Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 18.Problemas - Ex. 65

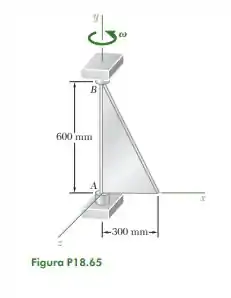
18.65. Uma placa triangular homogênea e fina de massa de 2,5 kg está soldada a um eixo vertical leve suportado por dois mancais em A e B. Sabendo que a placa gira com uma taxa constante de 8 rad /s, determine as reações dinâmicas nos pontos A e B.

Passo 1

Esse problema aqui vai fazer a gente relembrar duas equações do capítulo, as equações:

∑ F → = m a →

A segunda lei de Newton, e

∑ M A = H ˙ A A x y z + Ω × H A

E da imagem a gente pode ver que

ω → = 0   i ^ + ω   j ^ + 0   k ^

Passo 2

O próximo passo é calcular o momento de inércia. Bem a placa é triangular, então vamos definir b como a base do triângulo e h como a altura, sendo:

b = 300   m m h = 600   m m

Então

I y = 1 12 b 3 h

Esse é o momento de inércia de área. O momento de inércia de massa é o seguinte:

I y m = m A   I y

A área do triângulo é 1 2 b h , então

I y m = m ⋅ 2 b h ⋅   1 12 b 3 h

Isso fica

I y m = 1 6 m b 2

O produto de inércia do triângulo também é um valor conhecido:

I x y = 1 24 b 2 h 2

E o produto de inércia da massa

I x y m = m A I x y

Isso fica

I x y m = m ⋅ 2 b h ⋅ 1 24 b 2 h 2

Então

I x y m = 1 12 m b h

Agora vamos usar a equação 18.13:

H A = I x ω x - I x y ω y - I x z ω z i ^ + - I y x ω x - I y ω y - I y z ω z j ^

Substituindo os valores de ω

H A = I x 0 - I x y ω - I x z 0 i ^ + - I y x 0 - I y ω - I y z 0 j ^

Agora vamos substituir os valores de I .

H A = - 1 12 m b h ω i ^ + - 1 6 m b 2   ω

Isso fica

H A = - 1 12 m b h ω i ^ + - 1 6 m b 2 ω j ^

Passo 3

No nosso referencial rotacional podemos assumir

Ω = ω

E como não há uma aceleração angular

H ˙ A A x y z = 0

Isso vai facilitar bastante para gente. Agora vamos usar a equação que a gente relembrou lá no comecinho do problema.

∑ M A = H ˙ A A x y z + Ω × H A

Isso fica

∑ M A = 0 + ω × H A

∑ M A = ω × H A

Então

∑ M A = ω   j ^ × - 1 12 m b h ω i ^ + - 1 6 m b 2 ω j ^

Isso fica

∑ M A = 1 12 m b h ω 2 k ^ + 0

Vamos ver os momentos que agem no triângulo:

As forças em A não importam para gente agora porque vamos calcular o momento exatamente em A.

∑ M A = h   j ^ × B x   i ^ + h   j ^ × B y   k ^

Isso fica

∑ M A = - h B x   k ^ + h B z   i ^  

Então temos

- h B x   k ^ + h B z   i ^ = 1 12 m b h ω 2 k ^

Se nós separarmos por coeficiente temos

h B z = 0

Isso implica

B z = 0

E no coeficiente k ^

- h B x   = 1 12 m b h ω 2

Isso implica

B x = - 1 12 m b ω 2

E assim sabemos que a força B → é

B → = - 1 12 m b ω 2   i ^

Passo 4

Agora podemos usar a segunda lei de Newton:

∑ F → = m a →

Isso fica

A → + B → = m - x C M ω 2   i ^

O x C M do triângulo fica exatamente em x = b 3 .

Então

A → = - 1 3 m b ω 2 i ^ - - 1 12 m b ω 2   i ^

Finalmente temos

A → = - 1 4 m b ω 2   i ^

Passo 5

Já encontramos as equações para A → e B → , agora tudo que precisamos fazer para terminar o problema é substituir os valores. Do enunciado sabemos que

m = 2,5   k g ω = 8 r a d s b = 300   m m = 0,3   m h = 600   m m = 0,6   m

Então

A → = - 1 4 m b ω 2   i ^

A → = - 1 4 2,5 0,3 8 2   i ^ = - 12   i ^ N

E

B → = - 1 12 m b ω 2   i ^

B → = - 1 12 2,5 0,3 8 2   i ^ = - 4   i ^ N

E terminamos mais um!

Passo 6

Agora vamos calcular a mesma coisa, mas no referencial fixado G x y z

H ˙ G = H ˙ G G x ' y ' z ' + Ω × H G

Vamos primeiro resolver Ω × H G para não ficar uma equação gigante.

Ω × H G = [ - ω sin ⁡ β i ^ + ω cos ⁡ β )   j ^ × - 1 4 m r 2 ω sin ⁡ β i ^ ' + 1 2 m r 2 cos ⁡ β   j ^ '

Isso fica

= 1 4 m r 2 ω 2 cos ⁡ β sin ⁡ β   k ^ + - 1 2 m r 2 ω 2 sin ⁡ β cos ⁡ β k ^

= - 1 4 m r 2 ω 2 sin ⁡ β cos ⁡ β k ^

Agora vamos somar com H ˙ G G x ' y ' z '

H ˙ G = 1 4 m r 2 α sin ⁡ β cos ⁡ β i ^ + 3 4 m r 2 α sin 2 ⁡ β + cos 2 ⁡ β j ^ + - 1 4 m r 2 ω 2 sin ⁡ β cos ⁡ β k ^

Podemos colocar m r 2 em evidencia.

H ˙ G = m r 2 1 4 α sin ⁡ β cos ⁡ β i ^ + 3 4 α sin 2 ⁡ β + cos 2 ⁡ β j ^ - 1 4 ω 2 sin ⁡ β cos ⁡ β k ^

Beleza, chegamos em uma equação para H ˙ G , estamos quase acabando, só falta substituir o valor de β agora.

H ˙ G = m r 2 1 4 α sin ⁡ 25 ° cos ⁡ 25 ° i ^ + 3 4 α sin 2 ⁡ 25 ° + cos 2 ⁡ 25 ° j ^ - 1 4 ω 2 sin ⁡ 25 ° cos ⁡ 25 ° k ^

Fazendo todas essas contas temos

H ˙ G = m r 2 0,0958   α i ^ + 0,455   α j ^ - 0,0958   ω 2 k ^

E acabamos mais um!

Resposta

A → = - 12   i ^ N

B → = - 4   i ^ N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O disco A tem espessura constante e está em repouso quando posto em contato com a esteira BC, que se move com velocidade constante v. Indicado por μ k o coeficiente de atrito cinético entre o disco e
O volante de uma máquina perfuratriz tem uma massa de 300 kg e um raio de giração de 600 mm. Cada operação de perfuração requer 2.500 J de trabalho. (a) Sabendo que a velocidade do volante é de 300 rp
Dois discos de mesmo material estão presos a um eixo como mostrado na figura. O disco A tem raio r e espessura b, enquanto o disco B tem raio n r e espessura 3 b. Um binário M de intensidade constante
Resolva o Problema 17.12, considerando que a velocidade angular inicial do volante é 360 rpm no sentido horário.PROBLEMA 17.12 O tambor de freio de 160 mm de raio é preso a um volante maior que não es
O tambor de freio de 160 mm de raio é preso a um volante maior que não está mostrado na figura. O momento de inércia de massa total do volante e do tambor é 20 kg ∙ m2 e o coeficiente de atrito cinéti