Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 7

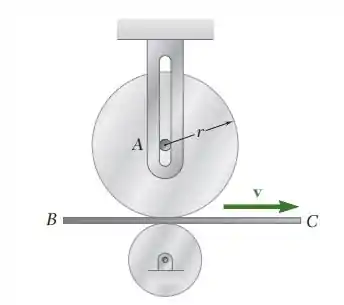
O disco A tem espessura constante e está em repouso quando posto em contato com a esteira BC, que se move com velocidade constante v. Indicado por μ k o coeficiente de atrito cinético entre o disco e a esteira, deduza uma expressão para o número de revoluções executadas pelo disco antes dele atingir uma velocidade angular constante.

Passo 1

E ai gurizada tudo belezinha??? O enunciado pede que a gente deduza uma expressão para o número de revoluções executadas pelo disco antes dele atingir uma velocidade angular constante

Passo 2

Trabalho da força de fricção externa no disco A.

Apenas a força que faz o trabalho é F. uma vez que seu momento sobre A é M = rF, temos:

U 1 → 2 = M θ = r F θ = r μ k   m g θ

Passo 3

Energia cinética do disco A.

A velocidade angular torna-se constante quando:

ω 2 = v r

T 1 = 0

T 2 = 1 2   I -   ω 2 2 = 1 2   1 2   m r 2 v r 2 = m v   ² 4

Passo 4

princípio de trabalho e energia para o disco A.

T 1 +   U 1 → 2 = T 2 :               0 + r μ k m g θ = m v ² 4

Mudança de Angulo:

θ = v ² 4   r   μ k g   r a d

Resposta

θ = v ² 8   π   μ k g   r e v

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A placa triangular mostrada na figura tem uma massa de 7,5 kg eestá soldada a um eixo vertical AB. Sabendo que a placa gira à taxaconstante 12 rad /s, determine a quantidade de movimento angular em re
Para o conjunto do Problema, determine (a) a quantidade de movimento angular em relação a B, (b) o ângulo formado entre a quantidade de movimento angular e o eixo BA.
Uma das esculturas expostas em um campus universitário consiste em um cubo oco feito de seis chapas de alumínio de 2 x 2 m cada, soldadas entre si e reforçadas com tirantes internos de massa desprezív
Se o cubo de alumínio do Problema fosse substituído por um cubo do mesmo tamanho, feito de seis placas de madeira compensada de massa de 10 kg cada um, quanto tempo levaria para fazer uma volta comple
Duas placas circulares, cada uma com massa 4 kg, são rigidamente conectadas pela barra AB de massa desprezível e suspensas pelo ponto A como mostra a figura. Sabendo que um impulso F∆ t = - 2,4N ∙ s k