Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 4.Problemas Fundamentais - Ex. 20
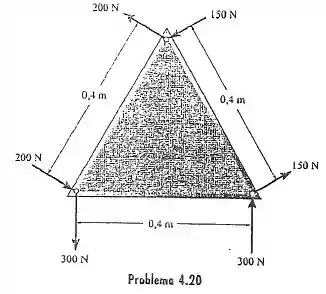
Determine o momento binário resultante que age sobre a chapa triangular.
Passo 1
Fala, querido!
Um momento binário é definido como duas forças paralelas que têm a mesma intensidade, mas direções opostas, e são separadas por uma distância perpendicular .
Note que o momento binário é um vetor livre, ou seja, pode agir em qualquer ponto, já que depende apenas do vetor posição, direcionado entre as forças.
Resumidamente, isso significa que apenas precisamos tratar apenas com uma das forças.
Vamos tratar o momento binário neste caso utilizando o analise escalar:
Onde é a intensidade das forças e é a distância perpendicular ao braço de momento entre as forças. (distância entre as linhas de ação de forças anti- paralelas)
Como queremos o momento binário resultante, a gente vai calcular todos os momentos binário e somar. Vamos adotar o sentido anti-horário como positivo. Bora!
Passo 2
Vamos olhar para as forças de . Repara que elas são anti-paralelas (paralelas em sentidos opostos) e a figura já dá a distância entre suas linhas de ação. Então basicamente já achamos :
Agora a gente precisa ver o sentido do momento gerado por elas. O momento segue o sentido das forças:
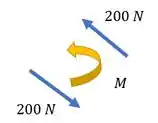
É um momento no sentido anti-horário né? Então ele vai ser positivo, aí usamos a fórmulinha:
Passo 3
Essa situação se repete para os outros dois binários. A figura já nos dá direto a distância :
E ambos causam momento também no sentido anti-horário. Então ambos serão positivos:
Passo 4
Para calcular o resultante a gente soma a galera toda que achamos: