Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 4.Problemas - Ex. 105
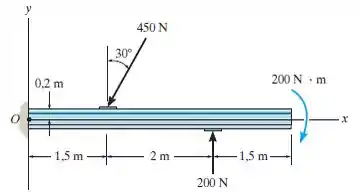
Substitua o sistema de carregamento que atua sobre a viga por uma força e um momento de binário resultantes equivalente no ponto .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
A ideia aqui é substituir as duas forças dadas no enunciado da questão por duas forças resultante e na direção (horizontal) e (vertical) e por um momento , todos em relação ao ponto .
Para isto, basta lembrarmos da seguinte relação:
Então, vamos aos cálculos!
Passo 2
Primeiramente, vamos determinar aqui . Para isto, temos que decompor a força de na direção . Detalhe que não precisamos nos preocupar com a força de pois ela é vertical! Portanto, temos:
Já para , temos:
Portanto, a força resultante é:
Uma força de formando um ângulo , medido no sentido anti-horário em relação a direção positiva do eixo .
Passo 3
Para finalizarmos, temos que calcular o momento em relação ao ponto . Para facilitar a nossa vida, como as forças estão inclinadas, em relação aos eixos coordenados, vamos trabalhar aqui com a forma vetorial.
Portanto, vamos calcular os momentos vetorialmente e depois fazer a soma deles. Começando pela força de , temos:
Já para a força de , temos:
E por fim, cuidado para não esquecerem do momento que está expresso no desenho da questão! Ah, lembrem-se que o momento é negativo quando ele rotaciona no sentido horário!
Portanto, o momento resultante é:
Com uma intensidade de no sentido horário (direção negativa do eixo ).
Resposta
Uma força formando um ângulo , medido no sentido anti-horário em relação a direção positiva do eixo , e um momento com uma intensidade de no sentido horário (direção negativa do eixo ).