Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 109
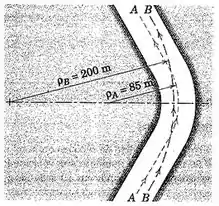
2/109 ) A figura mostra duas trajetórias possíveis para passar por uma curva sem inclinação lateral em uma parte horizontal de uma pista de corrida . A trajetória A-Asegue a linha central da estrada e tem um raio de curvatura , enquanto a trajetória B-B usa a largura da estrada para tirar vantagem em aumentar o raio de curvatura para . Se os motoristas limitam as suas velocidades em suas curvas de modo que a aceleração lateral não ultrapasse , determine a velocidade máxima para cada trajetória .
Passo 1
Bom pessoal , para resolvermos essa questão devemos lembrar da relação :
Dessa forma , obtemos que :
Resposta
Tranquilo galera? Bora para a próxima então
Exercícios de Livros Relacionados
2/122) O projeto de um sistema de comando de válvulas de um motor de autonóvel de quatro cilindors é mostrado. Quando o motor é acelerado , a velocidade da correia v varia uniformemente de 3 m / s até
2/119) Um foguete viajando acima da atmosfera a uma altitude de 500k m teria uma aceleração em queda livre g = 8,43 m / s 2 na ausência de outras forças que não a atração gravitacional . Devido ao emp
2/123) Adireção do movimento de uma fita plana em um dispositivo de controle numérico é alterada pelas duas polias A e B mostradas . Se a velocidade da fita aumenta uniformemente a partir de 2 m / s a
2/125) Uma fita magnética corre sobre a polia louca em um computador conforme mostrado . Se aceleração total de um ponto P sobre a fita em contato com a polia faz um ângulo de 4 ° com a tangente á fit
2/127) Para a bola de beisebol do Prob. 2/126 , determine o raio de curvatura ρ da trajetória e a taxa de variação no tempo v ' da nos instantes t = 1s e t = 2,5s onde t = 0 é o instante do lançamento