Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 119
2/119) Um foguete viajando acima da atmosfera a uma altitude de teria uma aceleração em queda livre na ausência de outras forças que não a atração gravitacional . Devido ao empuxo , no entanto , o foguete tem uma componente adicional de aceleração de tangente á sua trajetória , que faz um ângulo de com a verticalno instante considerado . Se a velocidade do foguete é de nessa posição , calcule o raio de curvatura da trajetória e a taxa em que está variando com o tempo .
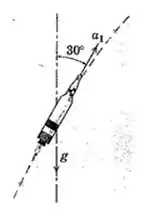
Passo 1
Bom galera , podemos achar a aceleração normal através da relação :
Passo 2
Agora para calcularmos o raio de curvatura da trajetória e a taxa em que está variando com o tempo , aplicamos as fórmulas :
Resposta
Exercícios de Livros Relacionados
O carro está viajando a uma velocidade escalar de 30m / s . O motorista, então, aciona os freios em A e, assim, reduz a velocidade escalar do carro a uma razão de a t = - 0,08 vm / s 2 , onde v é dado
Quando o carro chega ao ponto A, ele tem velocidade escalar de 25m / s . Se os freios são acionados, sua velocidade escalar é reduzida em a t = - 1 4 t 1 2m / s 2 . Determine a intensidade da aceleraç
Quando o carrinho de montanha-russa está em B, ele tem uma velocidade escalar de 25 m/s, a qual está aumentando em a t = 3m / s 2 . Determine a intensidade da aceleração do carrinho da montanha-russa
Um avião voa ao longo da trajetória circular horizontal AB em 60s . Se a sua velocidade escalar no ponto A é 120m / s , que diminui a uma razão de a t = - 0,03 tm / s 2 , determine a intensidade da ac
Determine a intensidade da aceleração do avião durante a curva. Ele voa ao longo da trajetória circular horizontal AB em 40s , enquanto mantém uma velocidade escalar constante de 90m / s .