Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 125

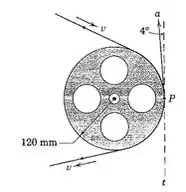
2/125) Uma fita magnética corre sobre a polia louca em um computador conforme mostrado . Se aceleração total de um ponto P sobre a fita em contato com a polia faz um ângulo de com a tangente á fita no instante quando a velocidade da fita é , determine o tempo necessário para levar a polia a parar com uma desaceleração constante . Considere que não ocorre escorregamento entre a polia e a fita .

Passo 1

Bom galera , primeiramente precisamos achar a aceleração normal . Para isso , usaremos :

Agora podemos calcular a aceleração tangencial através da relação :

Passo 2

Como constante , sabemos que :

Sendo assim , para acharmos o tempo necessário para levar a polia a parar , basta substituirmos os valores que conhecemos na fórmula :

Resposta

Suave pessoal? Então partiu fazer mais exercícios como esse!!!!!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um caminhão move-se ao longo de uma estrada circular que tem um raio de 50m a uma velocidade escalar de 4m / s . Por uma curta distância quando t = 0 , a sua velocidade escalar é, então, aumentada na

Um carro de corrida move-se com uma velocidade escalar constante de 240k m / h em torno de uma pista de corrida elíptica. Determine a aceleração sentida pelo motorista em B.

Uma partícula está se deslocando ao longo de uma curva tendo um raio de 20m . Se ela tem uma velocidade escalar inicial de 20m / s e em seguida começa a reduzir sua velocidade escalar na razão de a t

O avião a jato está se deslocando com uma velocidade escalar de 120m / s que está diminuindo a 40m / s 2 quando ele chega no ponto A. Determine a intensidade da sua aceleração quando ele está nesse po

A caixa de tamanho desprezível está deslizando para baixo ao longo de uma trajetória curva definida pela parábola y = 0,4x 2 . Quando ela está em A ( x A = 2m ,y A = 1,6m ) , a velocidade escalar é v