Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 123
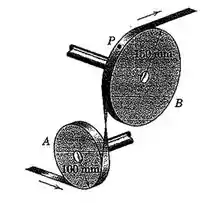
2/123) Adireção do movimento de uma fita plana em um dispositivo de controle numérico é alterada pelas duas polias A e B mostradas . Se a velocidade da fita aumenta uniformemente a partir de até enquanto metros de fita passam sobre as polias , calcule o módulo da aceleração do ponto P sobre a fita em contato com a polia B no instante em que a velocidade da fita é de .
Passo 1
Bom pessoal, primeiramente vamos achar a aceleração tangencial usando a equação de Torricelli :
Passo 2
Além disso , podemos calcular a equação normal pela fórmula :
Sendo assim :
Agora para acharmos a aceleração total basta aplicarmos a fórmula :
Resposta
Tranquilo pessoal? Bora resolver mais questões então
Exercícios de Livros Relacionados
Um caminhão move-se com uma velocidade escalar de 4m / s ao longo de uma estrada circular que tem um raio de 50m . Por curta distância a partir de s = 0 , sua velocidade escalar é, então, aumentada na
Um motociclista desloca-se ao longo da curva a uma velocidade escalar constante de 9m / s . Determine a sua aceleração quando ele está localizado no ponto A. Despreze a dimensão e do motociclista para
Os garotos em um tobogã estão se movendo para baixo ao longo de uma curva que pode ser aproximada pela parábola y = 0,01 x 2 . Determine a intensidade da sua aceleração quando eles chegam ao ponto A,
O avião a jato está se deslocando com uma velocidade escalar constante de 110m / s ao longo da trajetória curva. Determine a intensidade da aceleração do avião no instante que ele chega ao ponto A y =
Um carro de corrida move-se com uma velocidade escalar constante de 240k m / h em torno de uma pista de corrida elíptica. Determine a aceleração sentida pelo motorista em A.