Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 166

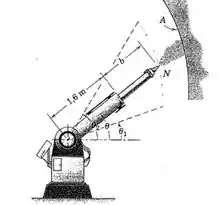
2/166) O robô de pinstura é programada para pintar uma linha de produção de superfícies curvas A( vista da borda ) . Ocomprimento do braço telescópico é controlado de acordo com b = 0,3 sen ⁡ π t 2 , onde b é em metros e t em segundos . Simultaneamente , o braço é programado para girar de acordo com θ = π 4 + π 8 sen ⁡ ( π t 2 ) radianos . Calcule o módulo v da velocidade do bocal N e o módulo a da aceleração de N para t = 1 s e para t = 2 s .

Passo 1

Então pessoal , organizando as informações que nós temos , obtemos que :

r = 1,6 + 0,3 sen ⁡ π t 2 m       ;     θ = π 4 + π 8 sen ⁡ π t 2

r ' = 0,3 π 2 cos ⁡ π t 2 m s       ;     θ ' = π 2 16 cos ⁡ π t 2   r a d / s

r " =  -0,3 π 2 4 sen ⁡ π t 2  m/ s 2  ;   θ " = - π 2 32 sen ⁡ π t 2   r a d / s 2  

Sendo assim , podemos econtrar as componentes da velocidade e da aceleração através das fórmulas :

v r = r ' =   0,3 π 2 cos ⁡ π t 2

v θ = r θ ' = 1,6 + 0,3 sen ⁡ π t 2 π 2 16 cos ⁡ π t 2

a r = r " - r θ ' 2 = -0,3 π 2 4 sen ⁡ π t 2 -( 1,6 + 0,3 sen ⁡ π t 2 ) π 2 16 cos ⁡ π t 2 2  

a θ = r θ " + 2 r ' θ ' = ( 1,6 + 0,3 sen ⁡ π t 2 ) ( - π 2 32 sen ⁡ π t 2 ) + 2 ( 0,3 π 2 cos ⁡ π t 2 ) ( π 2 16 cos ⁡ π t 2 )  

Passo 2

Agora tudo fica mais fácil! Para acharmos o valor da velocidade e da aceleração , basta substituirmos o valor de t nas equações de suas componentes e calcular o seu módulo :

Quando = 1 s :

v r = 0 v θ = 0 v = v r 2 + v θ 2 = 0

a r = - 0,740   m / s 2 a θ = - 1,841   m / s 2 a = 0,740 2 + 1,841 2 = 1,984   m / s 2

Quando = 2   s :

v r = - 0,471   m / s v θ = 0,987   m / s v = 1,094   m / s

a r = - 0,609   m / s 2 a θ = 0,581   m / s 2 a = 0,842   m / s 2

Resposta

Quando = 1 s :

v = 0

a = 1,984   m / s 2

Quando = 2   s :

v = 1,094   m / s

a = 0,842   m / s 2

Tranquilo galera? Bora resolver mais questões então!!!!!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a velocidade escalar constante máxima que um carro de corrida pode ter se a aceleração do carro não pode exceder 7,5m / s 2 enquanto gira em uma pista tendo um raio de curvatura de 200m .
Um carro viaja ao longo de uma pista circular de raio 75m , e sua velocidade escalar por curto período de tempo 0 ≤ t ≤ 2s e v = 0,9 t + t 2m / s , onde t é dado em segundos. Determine a intensidade d
O barco move-se ao longo de uma linha reta com a velocidade escalar descrita pelo gráfico. Construa os gráficos s - t e a - s . Determine também o tempo necessário para o barco se deslocar a distancia
O anel de 2,5 kg desliza sobre a barra lisa, de maneira que quando ele está em A ele tem velocidade de 3 m/s. Se a mola à qual ele está ligado tem comprimento não deformado de 0,9 m e rigidez de k = 1
Uma partícula de 2 kg desloca-se ao longo de uma trajetória lisa horizontal definida por r = 1 4 t 3 + 2m , θ = t 2 4r a d Onde t é dado em segundos. Determine as componentes da força radial e transve