Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 83

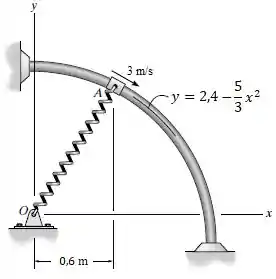
O anel de 2,5 kg desliza sobre a barra lisa, de maneira que quando ele está em A ele tem velocidade de 3 m/s. Se a mola à qual ele está ligado tem comprimento não deformado de 0,9 m e rigidez de k = 150 N/m, determine a força normal sobre o anel e aceleração dele neste instante.

Passo 1

O enunciado nos dá as seguintes informações:

Massa do anel: M = 2,5 kg;

Velocidade em A : v A = 3 m/s;

Rigidez da mola: k = 150 N/m;

Comprimento não deformado da mola: l 0 = 0,9 m;

Posição do ponto A : x = 0,6 m;

Trajetória curva;

Nosso objetivo é determinar a força normal e a aceleração do anel no instante em que ele passa pelo ponto A . Esta aceleração será uma combinação da aceleração tangencial com a aceleração normal.

Primeiramente, desenharemos o Diagrama de Corpo Livre do anel.

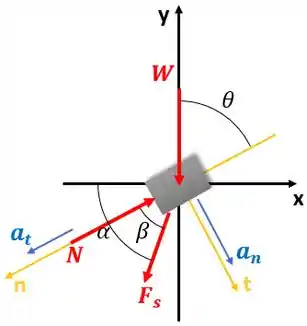
Onde W = força peso

N = força normal resultante

a t = aceleração tangencial

a n =aceleração normal

Lembre-se que a aceleração normal a n deve apontar no sentido positivo do eixo normal n . Como a aceleração tangencial a t é desconhecida, vamos supor que ela atue na direção de t positiva.

Sabemos que g = 9,81 m/s2 e que

W = M g

a t = d v d t

a n = v 2 ρ

ρ =   1 + d y d x 2 3 2 d 2 y d x 2

Onde ρ é o raio de curvatura no ponto onde o corpo está localizado.

Passo 2

Fazendo uma análise da geometria da situação, temos que

y = 2,4 - 5 3 x 2

d y d x = - 10 3 x

d 2 y d x 2 = - 10 3

Para o ponto x = 0,6 m:

ρ = 1 + d y d x 2 3 2 d 2 y d x 2 x = 0,6 = 1 + - 10 3 0,6 2 3 2 - 10 3 = 3,354

Passo 3

Em seguida, devemos encontrar o ângulo θ .

Olhando novamente o diagrama de corpo livre, podemos ver que

tan ⁡ θ = d y d x

Para o ponto x = 0,6 m:

θ = tan - 1 ⁡ d y d x x = 0,6 = tan - 1 ⁡ - 10 3 0,6 = - 63,435 °

O valor negativo serva para indicar o sentido em que o eixo girou em relação ao eixo de referência. Para o restante dos cálculos, utilizaremos o módulo de θ .

θ A = 63,435 °

Passo 4

Agora vamos descobrir quanto vale a Força Elástica exercida pela mola.

Primeiro, temos que encontrar o comprimento da mola no ponto A e o valor de y quando x = 0,6 m.

y = 2,4 - 5 3 0,6 2 = 1,8 m

O A = x 2 + y 2

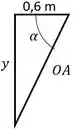
O A = 0,6 2 + 1,8 2 = 1,897 m

Sabemos que O A = l = 1,9 m e F s = k ∆ l , logo

F S = k ∆ l = k l - l 0

F s = 150 1,89 - 0,9 = 149,6 N

Agora precisamos saber a posição em que essa força atua. Analisando a geometria acima, vemos que

tan ⁡ α = y x = 1,8 0,6 = 3

α = 71,565 °

Porém, α é o ângulo que F s faz com o eixo de referência x-y. Queremos saber o ângulo β que esta força faz com o eixo n-t.

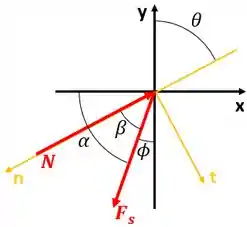
Logo,

90 ° - α = ϕ

ϕ = 18,435 °

θ - ϕ = β

β = 45 °

Passo 5

Agora utilizaremos a Equação do Movimento para encontrar a força normal N e a aceleração do anel no ponto A .

Aplicando a Equação do Movimento no sentido do eixo n , temos

∑ F n = m a n

W cos ⁡ θ - N + F s cos ⁡ 45 = M v 2 ρ

2,5 9,81 cos ⁡ 63,435 ° - N + 149,6 cos ⁡ 45 ° = 2,5 3 2 3,35

N = 110   N

Aplicando a Equação do Movimento no sentido do eixo t , temos

∑ F t = m a t

W sen ⁡ θ + F s sen ⁡ ( 45 ° ) = M a t

2,5 9,81 sen ⁡ 63,43 ° + 150 sen ⁡ 45 ° = 2,5 a t

a t = 51,20   m / s 2

Passo 6

Temos o valor de a t = 51,20 m/s2 e a n = 2,69 m/s2. Podemos encontrar o valor de a .

a = a n 2 + a t 2

a = 51,2 m/s2

Resposta

N = 110   N

a = 51,2   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os anéis estão conectados por um pino em B e estão livres para se mover ao longo da barra O A e da guia curvilínea O C , tendo o formato de uma cardinoide, r = 0,2 1 + cos ⁡ θ m. Em θ = 30 ° , a veloc
No instante que θ = 45 ° , o atleta está correndo com uma velocidade escalar constante de 2 m/s. Determine a velocidade angular na qual a câmera deve girar a fim de seguir o movimento.
A posição de uma partícula é descrita por r = t 3 + 4 t - 4 m e θ = t 3 / 2 rad, onde t é dado em segundos. Determine as intensidades da velocidade e aceleração da partícula no instante t = 2 s.
Uma partícula move-se ao longo de uma trajetória circular de raio 300 mm. Se sua velocidade angular é θ ˙ = 2 t 2 rad/s, onde t é dado em segundo, determine a intensidade da aceleração da partícula qu
Uma partícula move-se ao longo de uma trajetória circular de raio 5 m. Se sua posição é θ = e 0,5 t rad, onde t é dado em segundos, determine a intensidade da aceleração da partícula quando θ = 90 ° .