Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 167
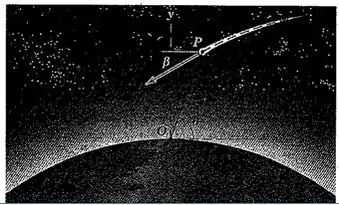
2/167) Um meteoro é rastreado por um radar observatório sobre a terra em . Quando o meteoro está diretamente acima () , as seguintes observações são registradas : , e . (a) determine a velocidade do meteoro eo ângulo que seu vetor velocidade faz com ahorizontal . Despreze quaisquer efeitos devido a rotação da terra. (b) repita com todas as quantidade dadas permanecendo iguais , exceto que .
Passo 1
Então pessoal , primeiramente vamos das uma olhada na figura que ilustra o problema :
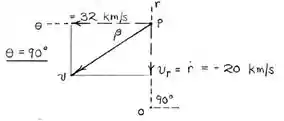
Com isso obtemos que :
Passo 2
Agora vamos entender o problema nessa nova configuração :
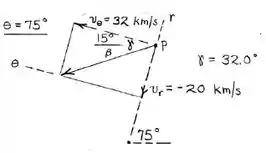
Reparem que as componentes da velocidade não se alteram , logo , o seu valor permanece constante :
Usando a trigonometria básica , temos que :
Sendo assim , achamos que :
Resposta
Para :
Para :
De boa pessoal? Bora resolver mais exercícios então