Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 146
2/146) A posição radial de umapartícula P de fluido em umadeterminada centrífuda com palhetas radiais é aproximada por , onde é tempo e é a velocidade angular constante na qual o impelidor gira . Determine a expressão para o módulo da aceleração total da partícula pouco antes de deixar as palhetas em termos de , e .
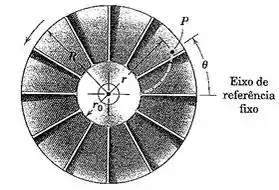
Passo 1
Então galera , nós sabemos que :
Além disso , nós temos que :
Sendo assim ,
Passo 2
Bom pessoal , utilizando trigonometria básica , sabemos que :
Dessa forma , quando , temos que :
Então , no instante que deixa as palhetas :
Resposta
Suave pessoal? Então partiu fazer mais exercícios como esse!!!!!
Exercícios de Livros Relacionados
2/148) Um satélite m se desloca em uma órbita elíptica em volta da terra . Não há nenhuma força sobre o satélite na direção θ , de modo que a θ = 0 . Prove que a segunda lei de Kepler do movimento pla
2/163) O braço com rasgo é articulado em O e sustenta o cursor C . Aposição de C no rasgo é determinada pelo cordão que está preso em D e permanece esticado . O braço gira no sentido anti-horário com
2/160) O disco circular gira em torno de seucentro O com uma velocidade angular constante ω = θ ' e carrega os dois êmbolos com mola mostrados . A distância b que cada êmbolo se projeta a partir da bo
2/162) O braço robótico é elevado e prolongado simultaneamente . Num determinado instante , θ = 30 ° , θ ' = 10g r a u s s=c o n s t a n t e , l = 0,5m , l ' = 0,2 m / s e l " = - 0,3 m / s ^ 2 . Calc
2/157) Um foguete segue uma trajetória no plano verrtical e é rastreado por radar a partir do ponto A . Em um determinado instante , as medições do radar fornecem r = 10,5k m , r ' = 480 m / s , θ ' =