Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 153
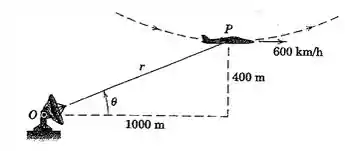
2/153) Na parte inferior de uma acrobacia aérea na qual o avião descreve um círculo em um plano vertical () a uma altitude de metros , o avião tem uma velocidade horizontal de e nenhuma aceleração horizontal . O raio de curvatura da trajetória é . Para o radar de rastreamento em , determine os valores de e registrados para esse instante .
Passo 1
Bom galera, a distância entre o radar e o avião é facilmente obtida por :
O ângulo de observação , por sua vez , é calculado por :
Sendo assim , para determinar os valores de e , usaremos que :
Resposta
Exercícios de Livros Relacionados
2/161) Uma locomotiva está viajando em uma estrada de ferro reta e horizontal com uma velocidade v = 90 k m / h e uma desaceleração a = 0,5 m / s 2 como mostrado . Em relação ao observador fixo em O ,
2/154) Uma aeronave voando em uma linha reta com um ângulo de ascensão β em relação à horizontal é rastreada por um radar localizado diretamente abaixo da linhade vôo . Em um determinado instante , os
O jogador de beisebol do Prob. 2/126 é repetido aqui com o fornecimento de informações adicionais. No instante t = 0 , a bola é arremessada com uma velocidade inicial de 30m / s em um ângulo de 30 ° e
Um satélite da Terra movendo-se na órbita elíptica mostrada tem uma velocidade v = 17970k m / h quando passa pela extremidade do semieixo menor em A . A aceleração do satélite em A é devida à atração
2/138) Um aeromodelo voasobre um observador O com velocidade constante em uma linha reta como mostrado . Determine os sinais ( mais , menos ou zero) para r,r ' ,r ",θ,θ 'eθ " para cada umadas posições