Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 22

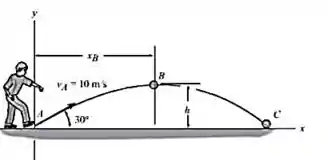
Uma bola é chutada do ponto A com a velocidade inicial v a = 10 m/s. Determine o alcance R e a velocidade escalar quando a bola tocar o solo.

Passo 1

Para o calculo de v c devemos, primeiramente, calcular o tempo necessário para que a bola alcance o ponto c , para isso podemos utilizar a equação horária do espaço.

Adotando a = - g

s = s 0 + v 0 t + 1 2 g t 2 → s A C = s A + v s e n 30 º - 1 2 g t A C 2

s A C = 0 , visto que não há variação de deslocamento entre os pontos A e C

Então t A C será

t A C = 1,0194 s

Passo 2

Para o calculo da velocidade v C , devemos calcular as componentes v x e v y , através das seguintes equações:

v C y = v A y - g t A C = 5 - 9,81 ( 1.0194 ) = - 5 m/s

v C x = V cos ⁡ 3 0 º = 10 cos ⁡ 3 0 º = 8,66 m/s

A resultante será

v c = v C x 2 + v C y 2 = ( - 5 ) 2 + ( 8,66 ) 2 = 10 m/s

Passo 3

Para o calculo do alcance máximo, basta utilizarmos a equação horária do espaço para MRU

s = s 0 + v t

Então, teremos

R = 0 + 8,66 ( 1,0194 ) = 8,83 m

Resposta

A velocidade em e o alcance R são, respectivamente 10 m/s e 8,83 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a velocidade escalar na qual uma bola de basquete em A deve ser jogada em um ângulo de 30° de maneira que ela chegue a cesta em B.
Um lançador de beisebol, joga a bola horizontalmente com uma velocidade escalar de 42m/s. se o rebatedor está a 18 m de distância, determinar o tempo que a bola leva para chear até ele e a altura h em
Um bombeiro segura a mangueira a um ângulo θ = 30 ° com a horizontal, e a água é lançada da mangueira em A com uma velocidade de v a = 12m / s . Se a corrente de água atinge o prédio em B , determine
Uma motocicleta deixa a rampa movendo-se a 33m / s , determine a altura h que a rampa B deve ter de maneira que a motocicleta pouse seguramente.
A bola é lançada em A e atinge o solo em B em 3s. determinar a intensidade da velocidade no momento em que a bola toca o solo, sua velocidade inicial va e o ângulo de inclinação em que ela foi jogada