Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 74
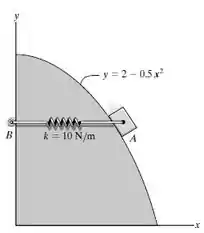
Um bloco de 6 kg está confinado a se mover ao longo da trajetória parabólica lisa. Uma mola ligada a ele restringe o movimento e, devido ao rolete-guia, sempre permanece horizontalmente à medida que o bloco desce. Se a mola tem uma rigidez de N/m, e comprimento não deformado de 0,5 m, determine a força normal da trajetória no bloco no instante m, quando o bloco tem uma velocidade de 4 m/s. Além disso, qual é a taxa de aumento da velocidade do bloco neste ponto? Despreze a massa do rolete e da mola.
Passo 1
Sabemos que a trajetória parábolica é conhecida e dada por:
Além disso, temos os seguintes dados:
massa do bloco: kg
rigidez da mola: N/m
comprimento não deformado da mola: m
velocidade em : m/s
gravidade: m/s2
Como a mola só varia de comprimento horizontalmente, em m o comprimento final da mola será m.
Analisando o enunciado, podemos ver que o problema envolve o movimento do corpo ao longo de uma trajetória curva conhecida. Quando temos este tipo de trajetória, é necessário traçar um novo eixo com as coordenadas normal e tangencial a fim de facilitar a resolução do problema. Assim, obtemos o seguinte diagrama de corpo livre:
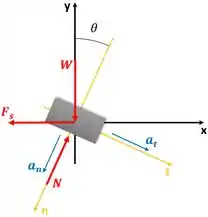
Onde = força peso
= força elástica
= força normal resultante
= aceleração tangencial
=aceleração normal
Como o enunciado diz que a trajetória é lisa, assumimos que a Força de Atrito é nula (=0).
Lembre-se que a aceleração normal aponta sempre para o sentido positivo do eixo .
Sabemos que
Onde é o raio de curvatura no ponto onde o corpo está localizado.
O problema pede para encontrarmos o valor de e .
Passo 2
Primeiramente, analisamos a geometria da situação.
Temos que
Logo, para m
Passo 3
Em seguida, devemos encontrar o ângulo .
Olhando novamente o diagrama de corpo livre, podemos ver que
Logo, para m, temos
Utilizaremos para desenvolver o restante do problema. O sinal de serve para mostrar apenas o sentido que o eixo girou em relação ao eixo de referência.
Passo 4
Agora, com os dados obtidos, utilizaremos as Equações de Movimento para encontrar a força e a taxa pedidas no enunciado.
Sabemos que
m
Aplicando a Equação do Movimento no sentido do eixo , temos
Aplicando a Equação do Movimento no sentindo do eixo , temos