Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas Fundamentais - Ex. 23
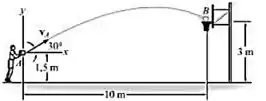
Determine a velocidade escalar na qual uma bola de basquete em A deve ser jogada em um ângulo de 30° de maneira que ela chegue a cesta em B.
Passo 1
Para o cálculo da velocidade em A, podemos utilizar a equação horária do espaço
Então, substituindo os valores na equação, encontraremos
Para encontrar o tempo em que a bola chega de A a B, podemos utilizar a equação do espaço para movimento horizontal
Então o tempo será:
Então velocidade será
Resolvendo a equação teremos
Resposta
A velocidade em A será de m/s
Exercícios de Livros Relacionados
Um foguete lançado verticalmente para cima a partir do pólo norte alcança uma velocidade de 27000k m / h em uma altitude de 350k m quando se esgota o seu combustível. Calcule a altura vertical adicion
Um objeto que é liberado a partir do repouso do topo A de uma torre de altura h parecerá não cair em linha reta devido ao efeito da rotação da Terra. Pode ser demonstrado que o objeto tem uma aceleraç
Um projétil é lançado com velocidade v 0 a partir do ponto A . Determine o ângulo de lançamento θ que resulta no alcance máximo R para cima do declive com ângulo α (onde 0 ≤ α ≤ 90 ° ). Avalie seus re
Um projétil é lançado a partir do ponto A com as condições iniciais mostradas na figura. Determine as coordenadas x e y do ponto de impacto.
Um projétil é lançado em um fluido experimental no instante t = 0 . A velocidade inicial é v 0 e o ângulo com a horizontal é θ . O arrasto sobre o projétil resulta em um termo de aceleração a D = - k