Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 24

2.24. Se a força resultante F R está orientada ao longo da linha a 75° no sentido horário a partir do eixo x positivo e a intensidade de F 2 deve ser mínima, determine as intensidades de F R e F 2 , e o ângulo θ ≤ 90 °

Passo 1

É importante notar que para F 2 ser mínimo, ele deve ser perpendicular a F R .

Logo podemos determinar θ da seguinte maneira

θ = 90 ° - 75 ° = 15 °

Passo 2

Vamos determinar a intensidade de F R somando sucessivamente as forças, quero dizer, a gente soma F 3 com F 1 e a gente obtém uma nova força F 13 , ai somamos F 13 com F 2 , então teremos F R .

Vamos começar somando F 1   e   F 3 .

Pela figura podemos perceber que o ângulo entre as forças é de 90°, então

F 13 = F 1 2 + F 2 2 = 4 2 + 5 2 = 6,403   k N

Repare que dessa soma podemos extrair esse triângulo

Então para determinar esse ângulo α

Sabemos que

tan ⁡ α = c a t e t o   o p o s t o c a t e t o   a d j a c e n t e = 5 4 Então

α = t a n - 1 5 4 = 51,34 °

Passo 3

Para descobrir F 2 vamos usar o fato que sabemos que F R   e   F 2 são perpendiculares, e podemos extrair esse triângulo

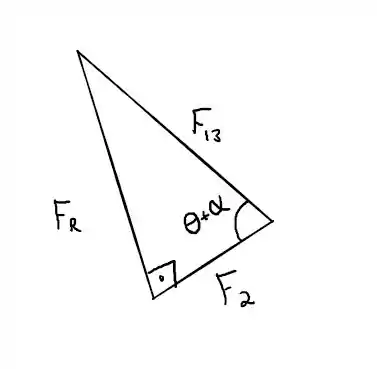
Então

F 2 = F 13 ⋅ cos ⁡ θ + α = 6,403 ⋅ cos ⁡ 15 ° + 51,43 ° = 2,57   k N

Desse mesmo triângulo podemos tirar que

F R = F 13 ⋅ sin ⁡ θ + α = 6,403 ⋅ sin ⁡ 15 ° + 51,43 ° = 5,86   k N

Resposta

F 2 = 2,57   k N

F R = 5,86   k N θ = 15 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas forças P e Q são aplicadas no ponto A de um suporte tipo gancho. Sabendo que P = 266N e Q = 110N , determine graficamente a intensidade, a direção e o sentido da resultante usando (a) a lei do pa
Duas forças P e Q são aplicadas no ponto A de um suporte tipo gancho. Sabendo que P = 75N e Q = 125N , determine graficamente a intensidade, a direção e o sentido da resultante usando (b) a regra do t
Para o tanque de aço do Problema 2.11, determine, usando trigonometria, (a) a intensidade e a direção da menor força P para qual a resultante R das duas forças aplicadas em A seja vertical, (b) a corr
Duas são aplicadas no ponto B da viga A B . Determine graficamente a intensidade, a direção e o sentido de sua resultante usando (a) a lei do paralelogramo.
Resolva o problema 2.4 usando trigonometria.