Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 2a
Duas forças P e Q são aplicadas no ponto de um suporte tipo gancho. Sabendo que e , determine graficamente a intensidade, a direção e o sentido da resultante usando (a) a lei do paralelogramo.
Passo 1
Bom galera, vamos começar usando a lei do paralelogramo para montar um triângulo com as nossas duas forças, e fica bem assim:
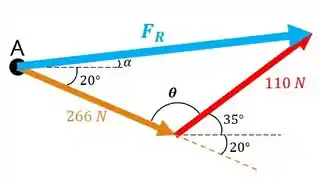
Obs.: Eu deixei assim na horizontal pra gente ver melhor, pra isso eu tive que girar em .
Passo 2
Belezinha, pra gente encontrar a força resultante que é a de azul usando a fórmula da lei dos cossenos a gente precisa do ângulo , que é bem simples, apenas:
Agora a lei do cossenos:
Passo 3
E para o ângulo a gente usa a lei dos senos rapidinho assim:
Fazendo aquele famoso esquema do “cruz credo”, a gente fica com:
Usando a função inversa do seno:
Lembrando que a gente usou o paralelogramo na horizontal (girando ) e ele tava na vertical, então:
Com o eixo .