Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 29

A ponte de 2 Mg, com centro de massa no ponto G, é levantada pelas duas vigas CD, localizadas em cada lado da ponte. Se o contrapeso E de 2 Mg estiver conectado às vigas como mostrado, determine o ângulo θ para equilíbrio. Despreze o peso das vigas e das barras de amarração.

Passo 1

Desenhando:

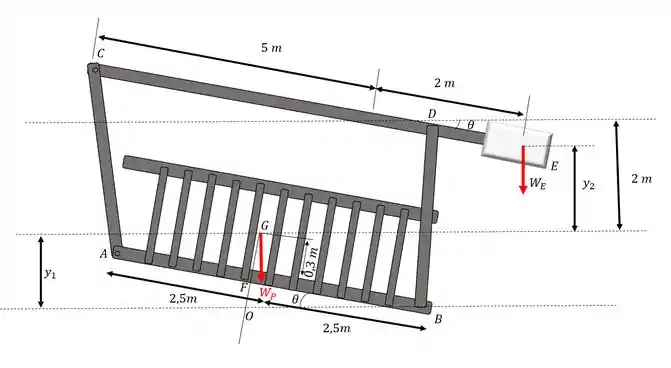
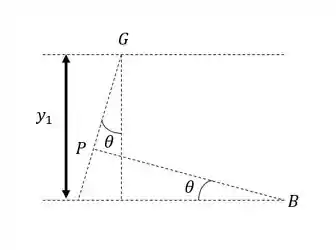
y 1 = G O ⋅ cos ⁡ θ = G F + F O c o s θ = G F + 0,3 c o s θ F O = 2,5 tan ⁡ θ y 2 = 2 - D E ⋅ s i n θ = 2 - 2 s e n θ

Passo 2

Vamos começar calculando a energia potencial:

V = V g p o n t e + V g c o n t r a p e s o

m b y 1 + m e y 2 V = 2000 0,3 c o s θ + 2,5 s e n θ + 2000 2 - 2 s e n θ V = 600 c o s θ + 1000 s e n θ + 4000

d V d θ = d d θ 600 c o s θ + 1000 s i n θ + 4000 d V d θ = - 600 s i n θ + 1000 c o s θ

Passo 3

Vamos calcular a posição de equilíbrio:

d V d θ = d d θ 600 c o s θ + 1000 s i n θ + 4000 d V d θ = - 600 s i n θ + 1000 c o s θ

Passo 4

Para calcular a estabilidade, precisamos calcular a segunda derivada:

d 2 V d θ 2 = d d θ ( - 600 s e n θ + 1000 c o s θ ) d 2 V d θ 2 = - 600 cos ⁡ 59,03 º - 1000 sen ⁡ 59,03 º < - 1166 ⇒   i n s t á v e l

Resposta

θ = 59,03 º

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

12. Resolva o Problema 11.11 se a força P for aplicada verticalmente para baixo no ponto B .
17.Uma mesa de servi uniforme de 5k g está apoiada em cada lado por dois pares de ligação, A B e C D , e molas C E . Se a tigela tem massa 1k g e está em equilíbrio quando θ = 45 ° , determine a rigid
16. Uma mesa de servi uniforme de 5k g está apoiada em cada lado por dois pares de ligação, A B e C D , e molas C E . Se a tigela tem massa 1k g , determine o ângulo θ onde a mesa está em equilíbrio.
15.A montagem é usada para exercício. Ela consiste em quatro barras conectadas por pinos, cada uma com extensão L e uma mola de rigidez k e comprimento livre a(2 L ) . Se forças horizontais são aplica
O mecanismo pantográfico está sujeito a uma força P=150 N. Determine o ângulo θ para o equilíbrio. A mola está livre em θ = 0 º º. Despreze a massa dos membros.