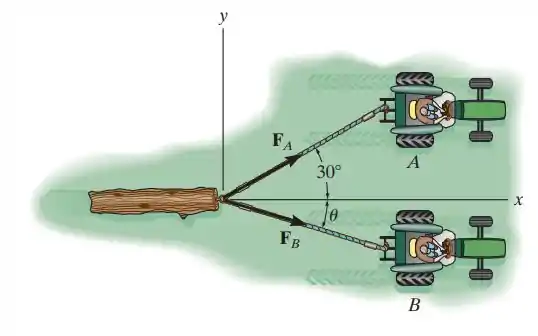
2.27. A resultante das duas forças que atuam sobre a tora deve estar orientada ao longo do eixo x positivo e ter uma intensidade de . Determine o ângulo θ do cabo acoplado a B para que a intensidade da força nesse cabo seja mínima. Qual é a intensidade da força em cada cabo, nessa situação?
Passo 1
Para ser mínimo, deve ser perpendicular a .
Vamos analisar os vetores , e como vetores, e aí poderemos usar a lei dos paralelogramos, vou desenhar isso.
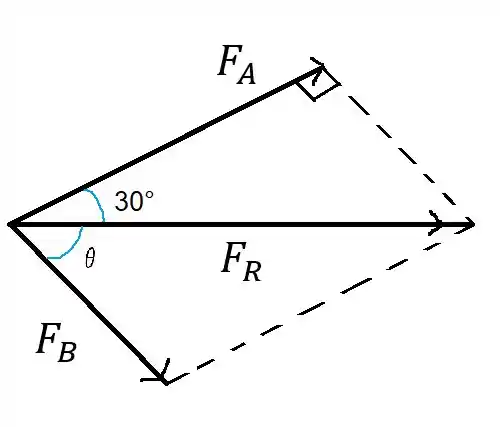
Daqui podemos extrair o seguinte triângulo
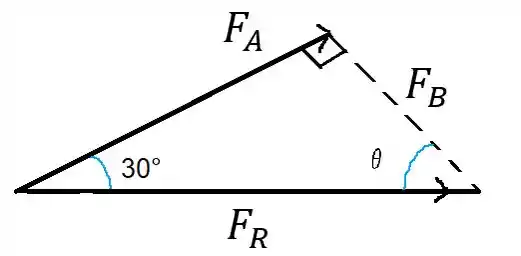
Passo 2
Para determinar a intensidade da força vamos usar trigonometria
Passo 3
Agora para calcular o ângulo θ, vamos usar a propriedade que diz que a soma dos ângulos internos de um triângulo é 180°.