Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 2.Problemas - Ex. 18

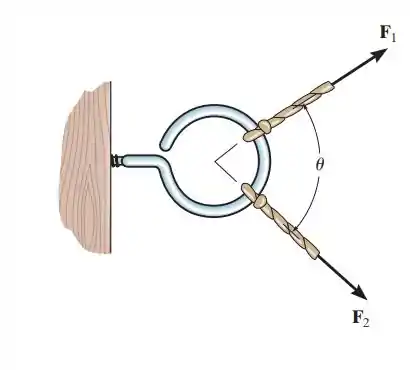
2.25. Duas forças F 1   e   F 2 atuem sobre o gancho. Se suas linhas de ação formam um ângulo θ e a intensidade de cada força é F 1 = F 2 = F , determine a intensidade da força resultante F R   e o ângulo entre F R   e   F 1 .

Passo 1

Vamos analisar os vetores F 1 , F 2 e F R   como vetores, e aí poderemos usar a lei dos paralelogramos, vou desenhar isso.

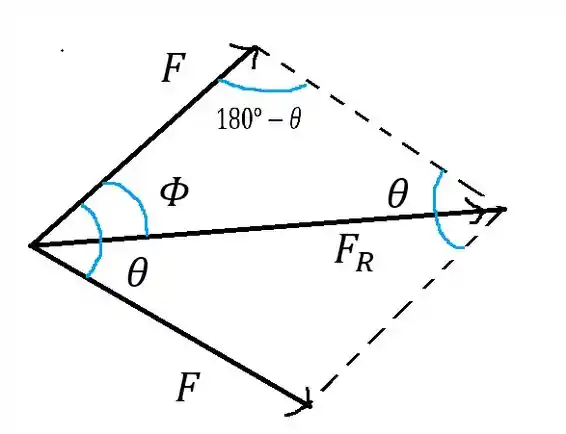
Daqui podemos extrair o seguinte triângulo

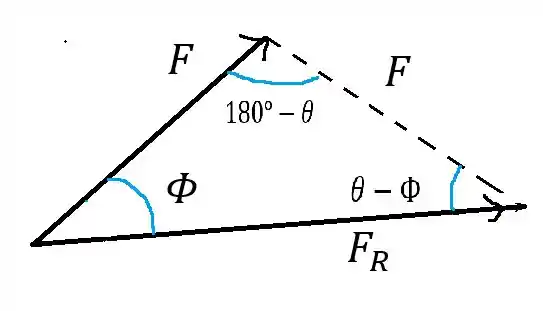
Passo 2

Vamos começar calculando o ângulo, usando a lei dos senos

F sin ⁡ Φ = F sin ⁡ θ - Φ sin ⁡ θ - Φ = sin ⁡ Φ θ - Φ = Φ Φ = θ 2

Passo 3

Agora podemos calcular a intensidade de F R usando a lei dos cossenos

F R = F 2 + F 2 - 2 ⋅ F ⋅ F ⋅ cos ⁡ 180 ° - θ

Lembrando que

cos ⁡ ( 180 ° - θ ) = - cos ⁡ θ

E que

c o s 2 θ = 1 + cos ⁡ θ 2

Então

F R = F ⋅ 2 ⋅ 1 + cos ⁡ θ 2

Como

1 + cos ⁡ θ 2 = cos ⁡ θ 2

Então

F R = 2 F ⋅ cos ⁡ θ 2

Resposta

Φ = θ 2 F R = 2 F ⋅ cos ⁡ θ 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2.1. Se θ = 6 0 ° e T = 5 k N , determine a intensidade da força resultante que atua sobre a argola e sua direção, medida no sentido horário a partir do eixo x positivo.
2.7. Se F B = 2k N e a força resultante atua ao longo do eixo u positivo, determine a intensidade da força resultante e o ângulo θ.
2.9. A chapa está submetida a duas forças em A e B, como mostrado na figura. Se θ = 60 ° , determine a intensidade da resultante das duas forças e sua direção medida no sentido horário a partir da hor
2.4. Determine a intensidade da força resultante que atua sobre o suporte e sua direção medida no sentido anti-horário a partir do eixo u positivo.
Se a tração no cabo é 400N , determine a intensidade e a direção da força resultante que atua sobre a polia. Esse ângulo é o mesmo ângulo θ da linha AB no bloco do carretel.