Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 1.Problemas - Ex. 9

Para dois vetores

A = i + 2 j - k e B = - 2 i + 3 j + k

Encontre:

a ) A - B e |A - B|

b ) c o m p o n e n t e d e B a o l o n g o d e A

c ) â n g u l o e n t r e A e B

d ) A xx B

e ) ( A - B ) xx ( A + B )

Passo 1

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de matrizes, vetores e cálculo vetorial.

Item a

A - B = i + 2 j - k - (- 2 i + 3 j + k) = 3 i - j - 2 k

|A - B| = sqrt(3^2 + (- 1)^2 + (- 2)^2) = sqrt(9 + 1 + 4) = sqrt(14)

Item b

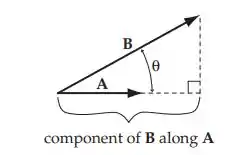
A componente B ao longo de A é Bcosθ. Do produto escalar temos:

A * B = A B c o s theta

= > B c o s theta = (A * B)/(A) = ((i + 2 j - k) * (- 2 i + 3 j + k))/(sqrt(1^2 + 2^2 + (- 1)^2)) = (- 2 + 6 - 1)/(sqrt(6)) = (3)/(sqrt(6)) = (sqrt(6))/(2)

A direção é, obviamente, ao longo de A. Um vetor unitário na direção A é:

(1)/(sqrt(6)) (i + 2 j - k)

Logo, a componente de B ao longo de A é dada por:

(1)/(2) (i + 2 j - k)

Passo 2

Item c

cos theta = (A * B)/(A B) = ((i + 2 j - k) * (- 2 i + 3 j + k))/(sqrt(1^2 + 2^2 + (- 1)^2) * sqrt((- 2)^2 + 3^2 + (- 1)^2)) = (- 2 + 6 - 1)/(sqrt(6) * sqrt(14)) = (3)/(2 sqrt(7))

= > theta = a r c cos (3)/(2 sqrt(7)) tilde= 55,5 °

Item d

A xx B = |[[i,j,k],[1,2,-,1],[-,2,3,1]]| = 2 i + 3 k + 2 j + 4 k - j + 3 i = 5 i + j + 7 k

Item e

Do item A, já temos A – B. Precisamos determinar A + B:

A + B = i + 2 j - k - 2 i + 3 j + k = - i + 5 j

Daí temos que:

(A - B) xx (A + B) = |[[i,j,k],[3,-,1,-,2],[-,1,5,0]]| = 15 k + 2 j - k + 10 i = 10 i + 2 j + 14 k

Resposta

Ver passo a passo.

Exercícios de Livros Relacionados

Determine o peso, em newtons, de uma mulher cujo peso é de 125 libras. Ache, também, sua massa em slugs e em quilogramas. Determine teu próprio peso em newtons.
Demonstre que o volume comum aos cilindros de interseção definidos por x2 + y2 = a2 e x2 + z2 = a2 é V = 16a3/3.
Determine o valor da integral ∫ S A ∙ d a , onde A = xi – yj + zk e S é a superfície fechada definida pelo cilindro c2 = x2 + y2. A parte superior e a parte inferior do cilindro se encontram z = d e 0
Avalie a soma ∑ k ε i j k ε l m k (contendo 3 termos). consiclerando o resultado de todas as possíveis combinações de i, j, l, m, ou seja: a )i = j b )i = l c )i = m d )j = l e )j = m f )l = m g )i ≠