Enunciado
Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 1.Problemas - Ex. 36
Determine o valor da integral , onde A = xi – yj + zk e S é a superfície fechada definida pelo cilindro c2 = x2 + y2. A parte superior e a parte inferior do cilindro se encontram z = d e 0, respectivamente.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de matrizes, vetores e cálculo vetorial.
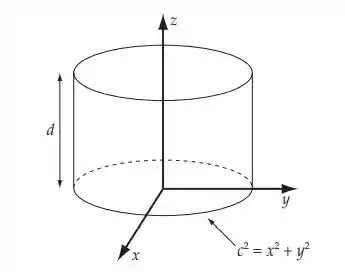
A forma da integral sugere o uso do teorema da divergência:
Como , precisamos apenas avaliar o volume total. Nosso cilindro tem raio c e altura d, então a resposta é:
Resposta
Ver passo a passo.
Exercícios de Livros Relacionados
Determine o valor da integral ∫ S A ∙ d a , onde A = (x2 + y2 + z2)(xi + yj + zk) e a superfície S é definida pela esfera R2 = x2 + y2 + z2. Calcule a integral diretamente e também utilizando o teorem
Demonstre que o produto escalar triplo A × B ∙ C pode ser escrito como A × B ∙ C = A 1 A 2 A 3 B 1 B 2 B 3 C 1 C 2 C 3 Demonstre também que o produto não é afetado por uma troca das operações de produ
Determine o valor da integral ∫ S ( ∇ × A ) ∙ d a , se o vetor A = yi + zj + xk e S é a superfície definida pelo parabolóide z = 1 – x2 – y2, onde z ≥ 0.
Derive as expressões a seguir utilizando álgebra vetorial: cos α - β = cos α cos β + s e nαs e nβ s e n α - β = s e nα cos β - cos α s e nβ
Encontre os componentes do vetor de aceleração a em coordenadas esféricas.