67. Se um torque ou momento de é necessário para afrouxar o parafuso em A, determine a força que precisa ser aplicada perpendicularmente ao cabo da chave de boca articulada.

Então temos que achar a força que gera o momento igual à . Para isso vamos usar a fórmula de calcular o momento e isolar a força, para conseguirmos saber seu valor.

Para resolver esse exercício vamos usar o método de análise escalar que é baseado na fórmula:

Onde d nesse caso é a distância perpendicular do braço do momento a parti do eixo da linha da força.

Para torna as coisas mais fáceis vamos adotar os eixos coordenados da seguinte maneira:

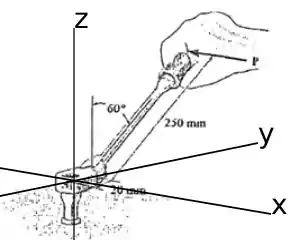
Então como nossa força deve ser perpendicular ao cabo, logo é perpendicular ao eixo y que adotamos então ela só tem a componente em x. O nosso eixo de rotação agora é o eixo z.

Como a chave faz um ângulo de 60° com o eixo z, necessariamente ela deve fazer um ângulo de 30° com eixo y, já que o ângulo entre z e y é 90°

Afigura nos fornece as distâncias em mm, mas passaremos elas para m, já que este é o mais usado.