Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 5

Determine a massa e a localização do centro de massa x -   da barra se sua massa por unidade de comprimento é m = m 0 ( 1 + x / L ) .

Passo 1

Vamos começar enxergando nosso elemento diferencial, ele é o comprimento do elemento mostrado na figura, nesse exercício precisamos apenas do eixo x .

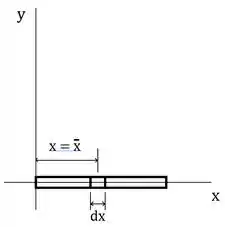
Vamos encontrar a massa da nossa barra integrando todos os pedacinhos d m ao longo dela:

m = ∫ m ⅆ m

Podemos escrever essa integral como:

∫ m ⅆ m = ∫ L m   d x

Assim, substituindo pela função dada no enunciado:

m = ∫ 0 L m 0 1 + x L ⅆ x =

Resolvendo essa integral temos nossa massa:

m = 3 2 m 0 L

Passo 2

Vamos agora para o centroide, sabemos que:

x - = ∫ x ⅆ m m

Então:

x - = ∫ 0 L x m 0 1 + x L ⅆ x m

x - = ∫ 0 L m 0 x 1 + x L ⅆ x m 0 3 2 L

x - = 2 3 L ∫ 0 L x + x 2 L ⅆ x

x - = 2 3 L x 2 2 + x 3 3 L 0 L

x - = 2 3 L L 2 2 + L 3 3 L

x - = 5 9 L

Resposta

x - = 5 9 L

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Localize o centroide x - da área.
A placa é feita de aço com uma densidade de 7850 kg/m³. Se a espessura da placa é 10 mm, determine as componentes horizontal e vertical da reação no pino A e a tração no cabo B C .
Localize o centroide y - da área.
Localize o centroide x - da área.
Localize o centroide x - da área.