Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas Fundamentais - Ex. 23

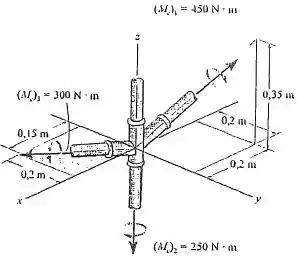
23.Determine o momento de binário resultante que age sobre o encanamento.

Passo 1

Para somar os momentos binários temos que passá-los para forma vetorial, para podermos somar corretamente cada componente dos momentos.

Para fazer isso, temos que calcular os vetores unitários que tem a mesma direção que cada momento e depois multiplicar cada momento por seu vetor unitário. Em linguagem matemática:

M → = M ⋅ u →

Sendo u → o vetor unitário com a mesma direção de M .

Passo 2

Vamos calcular o vetor unitário de cada momento um de cada vez.

Primeiro vamos calcular de M c 1 :

u 1 → = r 1 → r 1 →

Onde r 1 → é o vetor paralelo a M c 1 . Assim:

r 1 → = { - 0,2 i + 0,2 j + 0 , 35 k }

r 1 → = - 0,2 2 + 0,2 2 + 0 , 35 2

= 0 , 0 4 + 0,04 + 0 , 122

0,202 = 0,45

Logo:

u 1 → = { - 0,2 i + 0 , 2 j + 0 , 35 k } 0,45

= { - 2 4,5 i + 2 4,5 j + 3,5 4,5 k }

Vamos calcular de M c 2 :

u 2 → = r 2 → r 2 →

Onde r 2 → é o vetor paralelo a M c 2 . Assim:

r 2 → = { 0 i + 0 j - k }

r 2 → = 0 2 + 0 2 + - 1 2

= 0 + 0 + 1

1 = 1

Logo:

u 2 → = { 0 i + 0 j - k } 1

= { 0 i + 0 j - k }

Vamos calcular de M c 3 :

u 3 → = r 3 → r 3 →

Onde r 3 → é o vetor paralelo a M c 3 . Assim:

r 3 → = { 0 , 15 i - 0,2 j + 0 k }

r 3 → = 0 , 15 2 + - 0,2 2 + 0 2

= 0,0 22 + 0,04 + 0

0 , 06 2 = 0 , 25

Logo:

u 3 → = { 0,15 i - 0,2 j + 0 k } 0 , 2 5

= { 1,5 2,5 i - 2 2,5 j + 0 k }

Passo 3

Agora que temos os vetores unitários para cada momento, basta multiplicá-los pelos momentos, então:

  M c 1 → = M c 1 ⋅ u 1 →

M c 1 ⋅ u 1 → = 450 ⋅ { - 2 4,5 i + 2 4,5 j + 3,5 4,5 k }

= { - 200 i + 200 j + 350 k }

  M c 2 → = M c 2 ⋅ u 2 →

M c 2 ⋅ u 2 → = 2 50 ⋅ { 0 i + 0 j - k }

= { 0 i + 0 j - 25 0 k }

  M c 3 → = M c 3 ⋅ u 3 →

M c 3 ⋅ u 3 → = 30 0 ⋅ { 1,5 2,5 i - 2 2,5 j + 0 k }

= { 18 0 i - 2 4 0 j + 0 k }

Passo 4

Agora vamos somar os momentos para obter o momento resultante.

  M c R → =   M c 1 → +   M c 2 → +   M c 3 →

= - 200 i + 200 j + 350 k + 0 i + 0 j - 250 k + { 180 i - 240 j + 0 k }

= { - 20 i - 40 j + 100 k }

Resposta

O momento binário resultante é:

  M c R → = - 20 i - 40 j + 100 k   N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois parafusos A e B são apertados aplicando-se as forças e os binários mostrados na figura. Substitua os dois torsores por um torsor único equivalente e determine a a resultante R , b o passo do tors
Uma peça de chapa metálica é dobrada no formato mostrado e sofre a ação de três forças. Se as forças tem a mesma intensidade P , substitua as três forças por um torsor equivalente e determine a a inte
Dois parafusos A e B são apertados aplicando-se as forças e os binários mostrados na figura. Substitua os dois torsores por um torsor único equivalente e determine a a resultante R , b o passo do tors
Mostre que o torsor geralmente pode ser substituído por duas forças escolhidas de tal modo que uma força passa por um dado ponto enquanto a outra fica em um dado plano.
Substitua o torsor mostrado na figura por um sistema equivalente que consista em duas forças perpendiculares ao eixo y exercidas, respectivamente, em A e B ..