Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 143

Substitua o torsor mostrado na figura por um sistema equivalente que consista em duas forças perpendiculares ao eixo y exercidas, respectivamente, em A e B ..

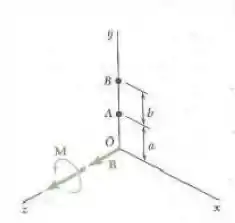
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos esboçar o diagrama de corpo livre do sistema equivalente:

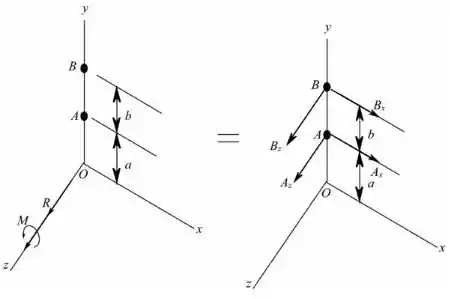
Passo 2

Agora, vamos expressar as forças A e B :

A = A x i + A z k

B = B x i + B z k

Vamos calcular as forças pra o sistema equivalente:

∑ F x = 0

A x + B x = 0

B x = - A x

E:

∑ F z = 0

A z + B z - R = 0

A z + B z = R

Passo 3

Vamos calcular o momento na direção x :

∑ M x = 0

A z a + B z a + b = 0

Agora em z :

∑ M z = 0

- A x a - B x a + b = M

Agora é só substituir as equações encontradas para resolver o sistema. Como B x = - A x , temos que:

B x a - B x a + b = M

B x b = - M

B x = - M b

Portanto:

A x = M b

Passo 4

Vamos agora descobrir o valor de A z .

A z a + B z a + b = 0

A z a + R - A z a + b = 0

A z = R a + b b

Portanto:

B z = R - R a + b b

B z = - a b R

Portanto, o vetor equivalente em A é:

M b i + R a + b b k

E o vetor equivalente em B é:

- M b i - a b R k

Resposta

O vetor equivalente em A é:

M b i + R a + b b k

E o vetor equivalente em B é:

- M b i - a b R k

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Expresse o momento do binário que age sobre o tubo na forma de vetor cartesiano. Qual é a intensidade do momento de binário? Considere F = 125N .
Se o momento de binário que age sobre o tubo tem uma intensidade de 300N ⋅ m , determine a intensidade F das forças aplicadas às chaves
Um binário atua sobre cada um dos manípulos da válvula minidual. Determine a intensidade e os ângulos diretores coordenados do momento de binário resultante.
As engrenagens estão sujeitas aos momentos de binário mostrados. Determine a intensidade do momento binário resultante e especifique seus ângulos diretores coordenados.
Se F 1 = 100N , F 2 = 120N e F 3 = 80 N , determine a intensidade e os ângulos diretores coordenados do momento de binário resultante.