Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 137
Dois parafusos e são apertados aplicando-se as forças e os binários mostrados na figura. Substitua os dois torsores por um torsor único equivalente e determine a resultante , o passo do torsor único equivalente, o ponto em que o eixo do torsor intercepta o plano .
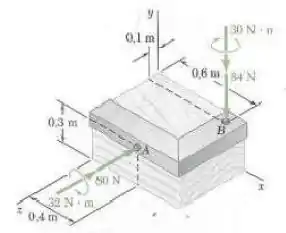
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
A resultante é dada pela soma das forças. Como estão em direções diferentes, vamos representar vetorialmente:
A magnitude é dada por:
Podemos então encontrar o vetor direção unitário:
Passo 2
O torsor equivalente é calculado ao fazer o produto vetorial dos vetores que ultrapassam a distância das linha de ação das forças ao ponto . Somados aos torsores iniciados:
Substituindo os valores, temos:
A intensidade do torsor na direção da pode ser calculada ao fazer o produto escalar entre o torsor e a direção de :
O passo do torsor é dado pela divisão entre a intensidade do torsor pela intensidade de :
Passo 3
Item c:
O torsor binário pode ser dado como o somatório dos torsores aplicados no sistema ou como o produto vetorial de por .
Portanto:
Portanto:
O eixo do momento torsor intercepta o plano em , e .