Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 35
2.35. O ponto de contato entre o fêmur e a tíbia está em A. Se uma força vertical de é aplicada nesse ponto, determine as componentes ao longo dos eixos x e y. Observe que a componente y representa a força normal na região da carga de rolamento dos ossos. As componentes x e y dessa força fazem com que o fluido sinovial seja comprimido para fora do espaço de rolamento.
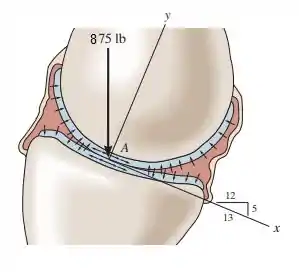
Passo 1
Nesse exercício só precisamos decompor o vetor força nos eixos x e y. O enunciado não nos dá nem um ângulo, mas nos dá esse triângulo
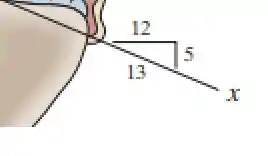
Vamos usá-lo para determinar os senos e cossenos.
Repare que podemos representar a figura usando o vetor
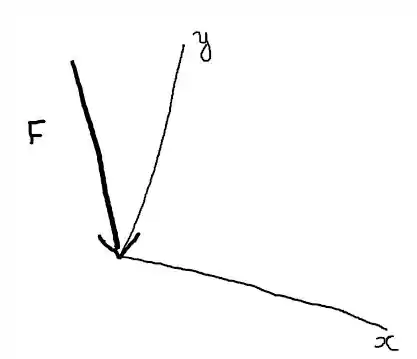
E isso é a mesma coisa que
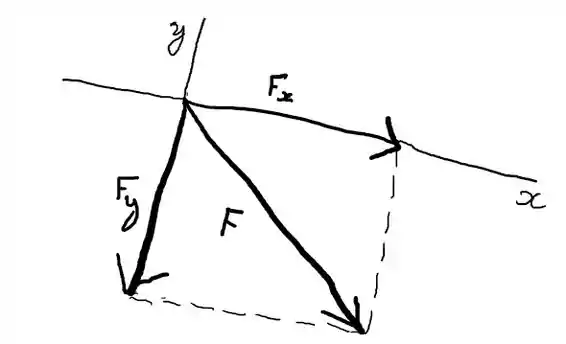
E daqui podemos extrair o triângulo
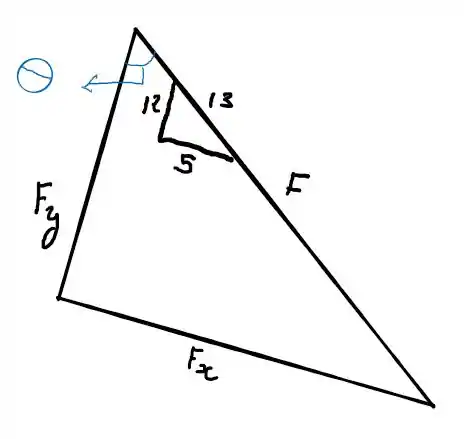
Passo 2
Vamos começar calculando .
Para calcular , você tem que reparar no triângulo da figura
Vamos lembrar que
Passo 3
Agora a gente usa a mesma estratégia para calcular determinar a força no eixo y
lembrando
está no sentido oposto ao eixo y, e por isso o sinal negativo.