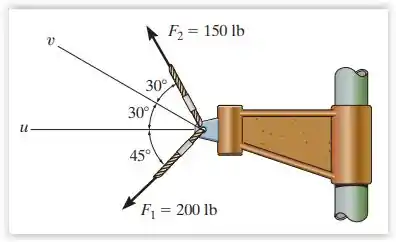
2.4. Determine a intensidade da força resultante que atua sobre o suporte e sua direção medida no sentido anti-horário a partir do eixo u positivo.
Passo 1
Repare que as forças são vetores, e para soma-los usaremos a lei dos cossenos.
Repare que θ é o ângulo entre as forças
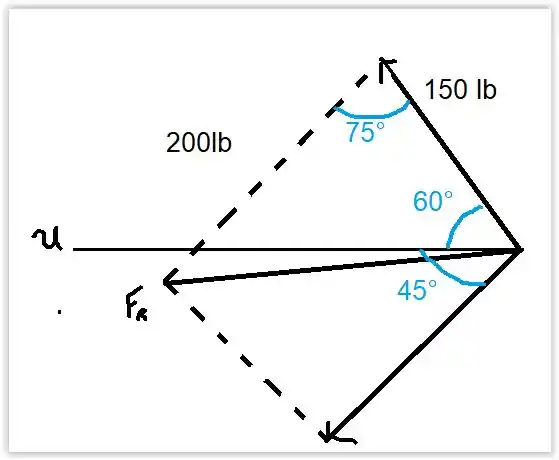
Passo 2
Agora basta calcular
Passo 3
Agora vamos determinar o ângulo da força, usando a lei dos senos.
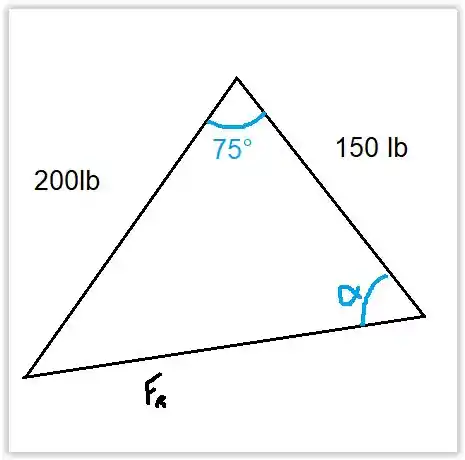
Então
Repare que , onde esse Φ é o ângulo da força resultante medida no sentido anti-horário de u
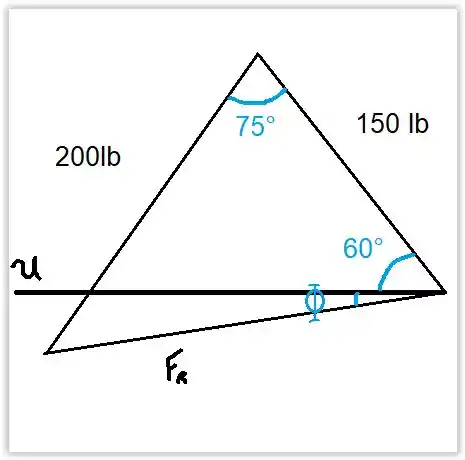
Então
Resposta
A intensidade da força é , e sua direção medida no sentido anti-horário do eixo u é .