Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 20
2.20. Se , e a força resultante é de , orientada ao longo do eixo y positivo, determine a intensidade necessária de e sua direção θ.
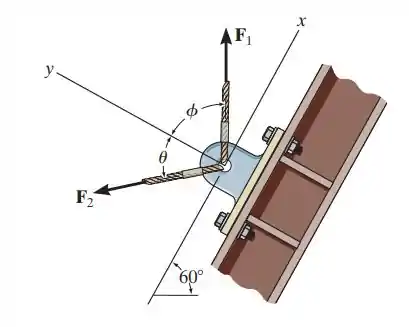
Passo 1
Falaaa, querido! Temos aqui um problema que pede para acharmos e sua orientação . Como a gente vai fazer isso? Cara, a gente pode usar a lei do paralelogramo.
Como ela funciona? Primeiro a gente desenha nossos vetores com suas orientações, num esqueminha. As forças são os lados vizinhos de um paralogramo e a resultante é o vértice.
Lembra que a resultante está na direção positiva de . Então ele fica entre e . Temos algo assim:
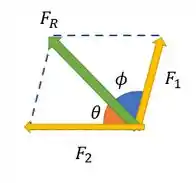
Por causa da simetria dos paralelogramos, podemos dizer que ângulos opostos são iguais. Isso faz com que o ângulo em frente a , tenha esse mesmo valor. E os ângulos dos outros dois vértices também sejam iguais. Aí pela soma interna de ângulos dos triângulos, podemos dizer que
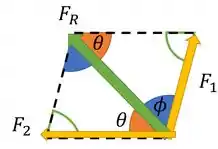
Daqui podemos extrair o seguinte triângulo
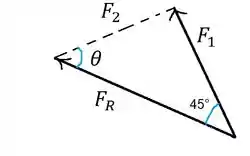
Isso porque Vamos seguir!
Passo 2
Agora temos tudo para determinar a intensidade de . Vamos usar a lei dos cossenos.
Ele nos deu os valores de e
Passo 3
Agora vamos usar a lei dos senos para determinar o ângulo θ.
Lembrando que na lei dos senos fazemos:
Aonde é o ângulo oposto ao lado e é o ângulo oposto ao lado .
No nosso caso, no triângulo da nossa figura, queremos encontrar o ângulo que é oposto a força e temos o ângulo de que é oposto a força .