Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 1.Problemas - Ex. 10
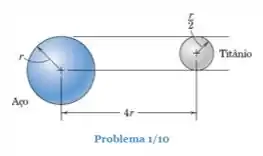
As esferas uniformes de aço e titânio são posicionadas conforme representado. Determine a magnitude da força gravitacional pequena de atração mútua se .
Passo 1
Oooi, tudo joinha?
Usando a lei da gravitação vamos determinar a magnitude da força gravitacional pequena de atração mútua das esferas de aço e de titânio.
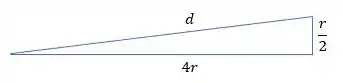
Observe que podemos encontrar a distância entre o centro das esferas usando o Teorema de Pitágoras:
Sabemos que, a densidade é igual a:
Então, para encontrar a massa, fazemos
A massa do Sol e da Terra são:
A constante de gravitação tem valor:
E o enunciado nos informa que
Passo 2
Agora só precisamos fazer as substituições:
Resposta
Exercícios de Livros Relacionados
Duas forças são aplicadas a um suporte tipo gancho indicadas na figura. Usando trigonometria e sabendo que a intensidade de P é 35N , determine (a) o ângulo requerido a se a resultante R das duas forç
Resolva o problema 2.2 usando trigonometria.
Para o suporte tipo gancho do Problema 2.7, sabendo-se que P = 75N e α = 50 ° , determine, usando trigonometria, a intensidade e a direção da resultantte das duas forças aplicadas no suporte.
Um tanque de aço deve ser posicionado em uma escavação. Sabendo-se que α = 20 ° , determine, usando a trigonometria, (a) a intensidade requerida para a força P se a resultante R das duas forças aplica
Um carrinho de mão que se movimenta ao longo da viga horizontal é acionado por duas forças indicadas na figura. (a) Sabendo-se que α = 25 ° , determine, usando trigonometria, a intensidade da força P