Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 4.Problemas Fundamentais - Ex. 24
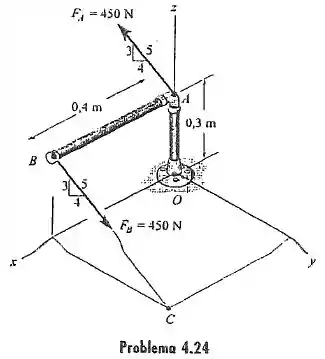
Determine o momento de binário que age sobre o encanamento e expresse o resultado como um vetor cartesiano.
Passo 1
Para determinarmos o momento binário, pensaremos da seguinte forma:
Os pontos e formarão um vetor vetor este que será nossa distância perpendicular à força.
Portanto para determinar o momento teremos uma multiplicação vetor comprimento e Força.
Resumidamente teremos a seguinte equação:
Representam as coordenadas do vetor posição definido a partir dos pontos e .
E , e são as componentes das nossas forças.
Passo 2
Vamos determinar o vetor :
Olhando para figura, podemos afirmar que as coordenadas do ponto é a seguinte:
E as coordenadas do ponto , fica o seguinte:
Considerando o ponto como inicial e o ponto como final do nosso vetor pode ser determinado, pela seguinte definição:
Substituindo os pontos, temos:
Passo 3
Temos o nosso vetor comprimento , agora temos que determinar as componentes cartesianas da nossa força:
Utilizaremos os pequenos triângulos de proporcionalidade, que foi nos dado pela figura.
Significa que utilizaremos semelhança de triângulos entre o triângulo feito pela força e o triângulo de números que foi nos dado.
Para a força aplicada no ponto :
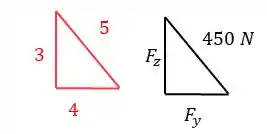
Para componente :
E , pois, não temos força atuando neste eixo.
Portanto, a nossa força fica o seguinte:
A componente é negativo, devido, o vetor estar apontando para baixo.
Passo 4
Finalmente podemos calcular nosso momento na sua forma cartesiana:
Executando o determinante, temos: