Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 4.Problemas - Ex. 133

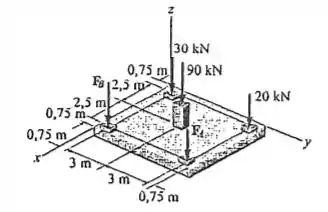
Se a força resultante deve agir no centro da placa, determine a intensidade das cargas das colunas F a   e   F b e a intensidade da força resultante.

Passo 1

A nossa força resultante deve atuar no centro da nossa placa, assim, devemos primeiramente encontrar onde fica esse centro que pela figura podemos observar que é em ( 3.75   ,   3.25 ) , além, disso a força resultante vai ser dada por

F r = ∑ F z →   - F r = - 30 - 20 - 90 - F a - F b

F r = 140 + F a + F b     ( i )

Passo 2

Agora, podemos encontrar o valor de F a     e   F b utilizando as equações de momento. Dessa forma, teremos

M r x = ∑ M x

→   - F r ⋅ ( 3,75 ) = - F b ⋅ 0,75 - 30 ⋅ 0,75 - 90 ⋅ 3,75 - 20 ⋅ 6,75 - F a ⋅ ( 6,75 )

→ F r = 0,2 ⋅ F b + 1,8 ⋅ F A + 132     ( i i )

M r y = ∑ M y

→   F r ⋅ 3 , 2 5 = F b ⋅ 5 , 75 + 30 ⋅ 0,75 + 90 ⋅ 3 , 2 5 + 20 ⋅ 0 , 75 - F a ⋅ ( 5 , 75 )

→ F r = 1,769 ⋅ F a + 1,769 F b + 101,54       ( i i i )

Resolvendo o sistema composto pelas equações i ,   i i   e   ( i i i ) encontraremos

F a = 30   k N ,   F b = 20 k N   e   F r = 190 k N

Resposta

F a = 30   k N ,   F b = 20 k N   e   F r = 190 k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o momento de binário que age sobre o encanamento e expresse o resultado como um vetor cartesiano.
23.Determine o momento de binário resultante que age sobre o encanamento.
72. Os efeitos do atrito do ar sobre as pás do ventilador criam um momento binário M 0 = 6N ⋅ m sobre as mesmas. Determine a intensidade das forças de binário na base do ventilador de modo que o momen
73. Determine a intensidade necessária dos momentos de binário M 2 e M 3 de modo que o momento de binário resultante seja zero.
91. Se M 1 = 500N ⋅ m , M 2 = 600N ⋅ m e M 3 = 450N ⋅ m , determine a intensidade e os ângulos de direção coordenados do momento de binário resultante.