Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 44

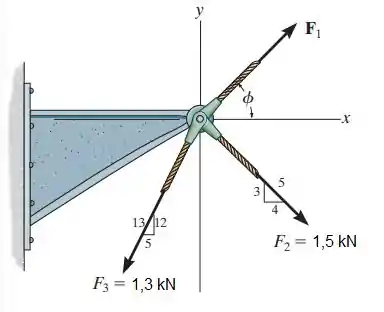
2.44. Se a intensidade da força resultante que atua sobre o suporte é 2   k N direcionada ao longo do eixo x positivo, determine a intensidade de F 1 e sua direção Φ

Passo 1

O exercício pede para que a gente calcule a intensidade de F 1 e determine sua direção. Para isso precisaremos decompor as forças nos eixos x e y e trabalhar com os vetores decompostos. Vamos começar a fazer isso pelo eixo x.

Passo 2

Vamos determinar a intensidade das forças no eixo x

F 1 x = F 1 ⋅ cos ⁡ Φ

Agora para determinar F 2 x vamos usar esse triângulo

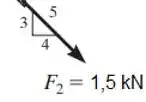
Repare que a imagem não nos dá um ângulo, mas nos dá esse triângulo. Vamos lembrar que sin ⁡ α = c a t e t o   o p o s t o h i p o t e n u s a = 4 5

Se pensarmos o ângulo α da seguinte forma

F 2 x = 1,5 ⋅ sin ⁡ α = 1,5 ⋅ 4 5 = 1,2   k N

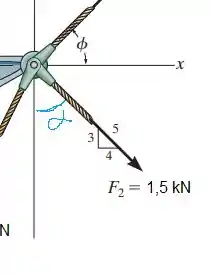
Vamos fazer algo parecido para determinar F 3 x

F 3 x = - F 3 ⋅ sin ⁡ γ = - 1,3 ⋅ 5 13 = - 0,5

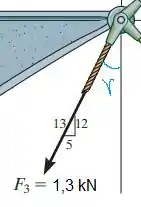
Repare que F 3 x está no sentido oposto de x

Agora podemos saber a resultante no eixo x

F R x = F 1 x + F 2 x + F 3 x = F 1 ⋅ cos ⁡ Φ + 1,2 - 0,5 = ( F 1 ⋅ cos ⁡ Φ + 0,7 )     k N

Mas o enunciado nos diz que a força resultante está toda no eixo x, então

( F 1 ⋅ cos ⁡ Φ + 0,7 )     k N = F R

F 1 ⋅ cos ⁡ Φ + 0,7 = 2

F 1 ⋅ cos ⁡ Φ = 1,3

Passo 3

Agora a gente calcula as forças no eixo y

F 1 y = F 1 ⋅ sin ⁡ Φ

Para calcular F 2 y   e   F 3 y vamos usar uma estratégia parecida com a que usamos para calcular F 2 x   e   F 3 x , mas agora ao invés de senos usaremos cossenos.

F 2 y = - 1,5 ⋅ cos ⁡ α = - 1,5 ⋅ 3 5 = - 0,9   k N

F 3 y = - F 3 ⋅ cos ⁡ γ = - 1,3 ⋅ 12 13 = - 1,2   k N

F R y = F 1 y + F 2 y + F 3 y = F 1 ⋅ sin ⁡ Φ - 0,9 - 1,2 = ( F 1 ⋅ sin ⁡ Φ - 2,1 )   k N

Mas o enunciado nos diz que a força resultante está toda no eixo x, então

( F 1 ⋅ sin ⁡ Φ - 2,1 )   k N = 0

F 1 ⋅ sin ⁡ Φ = 2,1

Passo 4

Agora temos duas variáveis ( F 1   e   Φ ), e duas equações.

F 1 ⋅ cos ⁡ Φ = 1,3

F 1 ⋅ sin ⁡ Φ = 2,1

Vamos elevar ambas as equações ao quadrado e soma-las para sumir com Φ

F 1 2 ⋅ cos 2 ⁡ Φ + F 1 2 ⋅ sin 2 ⁡ Φ = 1,3 2 + 2,1 2

F 1 2 ⋅ ( cos 2 ⁡ Φ + sin 2 ⁡ Φ ) = 6,1

F 1 = 6,1 = 2,47   k N

Passo 5

Agora podemos usar F 1 para descobrir Φ

F 1 ⋅ cos ⁡ Φ = 1,3

2,47 ⋅ cos ⁡ Φ = 1,3

Φ = c o s - 1 1,3 2,47 = 58,24 °

Resposta

F 1 = 2 , 47   k N Φ = 58,24 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A alavanca de controle O A gira na faixa 0≤θ≤90 ° . Uma mola de torção interna exerce um momento de retorno na alavanca em torno do ponto O , dado por M = K ( θ + π / 4 ) , em que K=500N·m m / r a deθ
Expresse e identifique a resultante das duas forças e um binário mostrado atuando no eixo em ângulo no plano x - z .
A mola que conecta o ponto B do disco e o ponto C na superfície vertical está sob uma tensão de 500N . Escreva essa tensão, pois ela atua no ponto B como um vetor de força T em termos dos vetores unit
2.3. Decomponha a força de 30N nas componentes ao longo dos eixos u e v, e determine a intensidade de cada uma dessas componentes.
Determine as resultantes e os cossenos diretores das resultantes dos sistemas de forças representados na figura abaixo.i)