Enunciado
Mecânica e Resistência dos Materiais - Estatica das Estruturas por Humberto Lima Soriano- Ed: 3º - Capítulo 1.9 - Ex. 1i
Determine as resultantes e os cossenos diretores das resultantes dos sistemas de forças representados na figura abaixo.
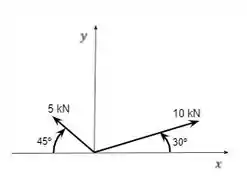
i)
Passo 1
Primeiro devemos realizar a decomposição das forças. Sendo assim, utilizaremos:
Consideraremos a fórmula acima e então substituiremos pelos, valores que possuímos, começando então pelo vetor de 10 kN e levando em conta que o problema trata de um sistema cartesiano xy, temos:
Já para o vetor de 5kN, teremos:
Passo 2
A resultante se dá pelo somatório de todas as forças, sendo assim temos:
Passo 3
Já os cossenos diretores se dão, pela fórmula abaixo:
Sendo assim, ao substituirmos teremos:
Resposta
1.i) 
; 0,50; 0,86
Exercícios de Livros Relacionados
A força F → atua ao longo de um elemento do cone circular direito, como mostrado. Determine o sistema de força-binário equivalente no ponto O.
Duas forças atuam na placa retangular, conforme mostrado. Reduza este sistema de forças a um sistema de força-binário equivalente atuando no ponto O. Em seguida, determine a resultante do sistema, exp
No instante mostrado quando os crankpins de um motor de dois cilindros passam pelo plano horizontal y - z , a haste A está sob uma compressão de 1,8k N e a haste B está sob uma compressão de 0,8k N .
A força de 180l b é aplicada no ponto A do suporte. Determine os momentos desta força sobre o ponto B, sobre o ponto C e sobre a linha B C - .
Substitua as duas forças e o binário simples por um sistema de força-binário equivalente no ponto A.