Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 46

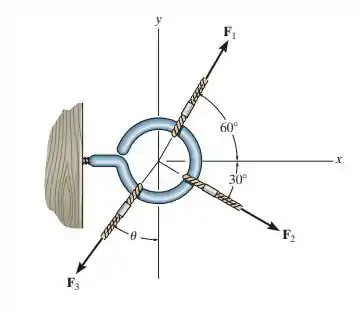
2.46. As três forças concorrentes que atuam sobre o olhal produzem uma força resultante F R = 0 . Se F 2 = 2 3 F 1 e F 1 precisa estar a 90 ° de F 2 , como mostra a figura, determine a intensidade necessária de F 3 expressa em função de F 1 e o ângulo θ .

Passo 1

Fala, querido!

O exercício pede para a gente achar a magnitude de F 3 em termos de F 1 . E a orientação de F 3 .

E para ajudar ele diz que a resultante F R é zero. Isso implica que as componentes dessa resultante também valem zero.

R x = 0

R y = 0

O que podemos fazer aqui é achar as componentes das forças que a gente tem no desenho, somar a galera de cada eixo, achando expressões para R x e R y . E depois igualar essas bonitas a zero, porque as componentes da resultante zeram.

Com isso a gente tem um sisteminha e acha o que enunciado pede. Vamos lá!

Passo 2

Vamos escrever nossas forças na forma vetorial. Isso vai nos dá as componentes em cada eixo. Repara que F 1 aponta para o sentido positivo dos dois eixos e o ângulo da sua orientação é oposto a y. Então o seno fica na componente y e ambas ficam positivas.

F 1 = F 1 ⋅ cos ⁡ 60 °   i + F 1 ⋅ sin ⁡ 60 °   j

F 1 = 0,5 ⋅ F 1   i + 0,866 ⋅ F 1   j

Como sabemos que F 2 = 2 3 F 1 , mas repare que F 2 é negativo no eixo y e o ângulo da sua orientação é oposto a y. Podemos determinar F 2 da seguinte maneira

F 2 = F 2 ⋅ cos ⁡ 30 °   i - F 2 ⋅ sin ⁡ 30 °   j

F 2 = 2 3 F 1 ⋅ cos ⁡ 30 °   i - 2 3 F 1 ⋅ sin ⁡ 30 °   j

F 2 = 2 3 3 2   ⋅ F 1   i - 2 3 1 2 ⋅ F 1   j

E vamos deixar F 3 de forma mais generalizada, repare que F 3 é negativo tanto em x quanto em y. E seu ângulo é oposto ao eixo x. Logo essa componente fica com o seno.

F 3 = - F 3 ⋅ sin ⁡ θ   i - F 3 ⋅ cos ⁡ θ   j

Passo 3

Agora vamos falar de F R . Sabemos que F R = 0 , então F R = 0   i + 0   j .

Por outro lado

F R = F 1 + F 2 + F 3

Então

F R x = F 1 x + F 2 x + F 3 x

F R y = F 1 y + F 2 y + F 3 y

Para achar essas componentes é só olhar para nossos vetores. Eles estão escritos na forma

F = F x   i ^ + F y   j ^

Agora nós temos tudo para determinar F 3 e θ , vamos começar por F 3 x , olha só

F R x = F 1 x + F 2 x + F 3 x

0 = 0,5 ⋅ F 1 + 2 3 3 2 ⋅ F 1 - F 3 ⋅ sin ⁡ θ

F 3 ⋅ sin ⁡ θ = 0,5 ⋅ F 1 + 0,5774 ⋅ F 1

F 3 ⋅ sin ⁡ θ = F 1 ⋅ ( 0,5 + 0,5774 )

F 3 ⋅ sin ⁡ θ = 1,077 ⋅ F 1

Agora vamos fazer o mesmo para F y

F R y = F 1 y + F 2 y + F 3 y

0 = 0,866 ⋅ F 1 - 2 3 1 2 ⋅ F 1 - F 3 ⋅ cos ⁡ θ

F 3 ⋅ cos ⁡ θ = 0,866 ⋅ F 1 - 0,3333 ⋅ F 1

F 3 ⋅ cos ⁡ θ = F 1 ⋅ 0,866 - 0,3333

F 3 ⋅ cos ⁡ θ = 0,5327 ⋅ F 1

Passo 4

Agora temos duas incógnitas ( F 3   e   θ ) e duas equações

F 3 ⋅ sin ⁡ θ = 1,077 ⋅ F 1

F 3 ⋅ cos ⁡ θ = 0,5327 ⋅ F 1

Vamos elevar ambas as equações ao quadrado e soma-las para sumir com θ

F 3 2 ⋅ sin 2 ⁡ θ + F 3 2 ⋅ cos 2 ⁡ θ = 1,077 2 ⋅ F 1 2 + 0,5327 2 ⋅ F 1 2

F 3 2 ⋅ ( sin 2 ⁡ θ + cos 2 ⁡ θ ) = F 1 2 ⋅ ( 1,077 2 + 0,5327 2 )

Lembrando da relação trigonométrica sin 2 ⁡ x + cos 2 ⁡ x = 1 , portanto:

F 3 2 × 1 = 1,443 ⋅ F 1 2

F 3 = 1,443 ⋅ F 1 2 = 1,2 ⋅ F 1

Passo 5

Agora vamos determinar θ

F 3 ⋅ sin ⁡ θ = 1,077 ⋅ F 1

1,2 ⋅ F 1 ⋅ sin ⁡ θ = 1,077 ⋅ F 1

1,2 ⋅ sin ⁡ θ = 1,077

sin ⁡ θ = 1,077 1,2

θ = s i n - 1 1,077 1,2 = 63,8 °

Resposta

F 3 = 1,2 ⋅ F 1 θ = 63,8 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para satisfazer limitações de projeto é necessário determinar o efeito da força trativa de 2k N atuando no cabo, sobre o cisalhamento, a tração e a flexão da viga em I engastada. Com este propósito, s
Determine os componentes da força de 2k N ao longo dos eixos oblíquos a e b . Determine as projeções de F sobre os eixos a e b .
Determine os componentes escalares R a e R b da força R ao longo dos eixos não retangulares a e b . Determine também a projeção ortogonal P a de R sobre o eixo a .
A razão entre a força de sustentação L e a força de arraste D , para um aerofólio simples, é L / D = 10 . Se a força de sustentação em uma seção curta do aerofólio vale 200N , calcule o módulo da forç
Deseja-se remover o pino da madeira pela aplicação de uma força ao longo de seu eixo horizontal. Um obstáculo A impede um acesso direto, de modo que duas forças, uma de 1,6k N e a outra P , são aplica