2.47. Determine a intensidade de e sua direção , de modo que a força resultante seja direcionada ao longo do eixo x positivo e tenha uma intensidade de .
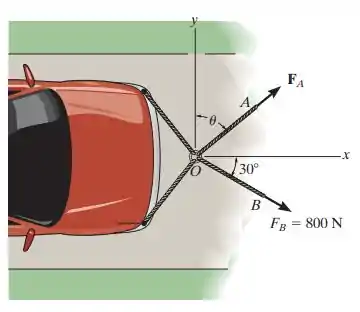
Passo 1
O exercício pede para a gente achar a magnitude de , e nos diz que , está ao longo do eixo x positivo.
A representação dessa imagem em vetores fica o seguinte
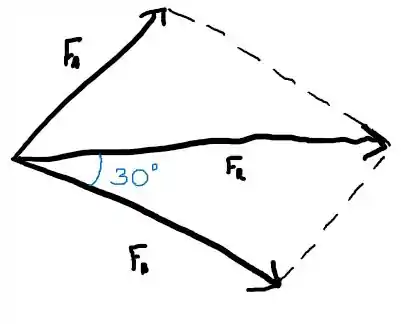
Para facilitar os cálculos vamos decompor os vetores em termos dos eixos x e y.
Passo 2
Vamos começar por
Mas o enunciado diz que a força resultante está ao longo do eixo x positivo, então
Passo 3
Agora vamos fazer a mesma coisa para
Mas o enunciado diz que a força resultante está ao longo do eixo x positivo, então
Passo 4
Agora temos duas incógnitas ) e duas equações
Vamos elevar ambas as equações ao quadrado e soma-las para sumir com
Passo 5
Agora vamos determinar