Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 22
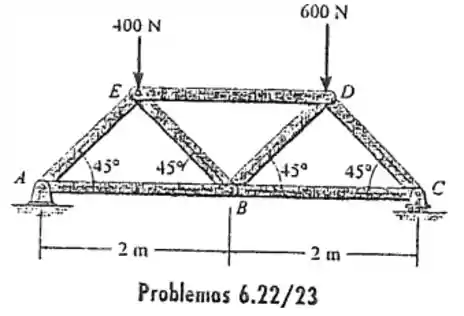
6.22 Determine a força em cada membro da treliça e indique se os membros estão sobre tração ou compressão.
Passo 1
Falaa!
Vamos usar o método dos nós abordado no começo do capitulo. Como não temos nenhum nó com uma força conhecida e no máximo duas forças incógnitas, vamos ter que calcular as reações externas nos apoios:
Vamos calcular o momento em C, pois dessa forma vamos obter direto a força A:
As forças em e em deveram ser iguais para manter o equilíbrio então:
Passo 2
Agora que temos um nó com apenas duas forças incógnitas e uma força conhecida conseguimos começar a descobrir as forças de cada membro. Analisando, então, o nó A:
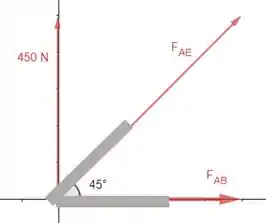
Vamos montar as equções para :
O sinal negativo indica que adotamos a direção errada para essa força, então na verdade A força AE é uma força de compressão, está entrando na seção da barra
Agora para o eixo :
O sinal ficou positivo, então a força foi adotada corretamente, podemos escrever:
Pois como indica o diagrama, essa força está tracionando o membro AB, já que a força está saindo da seção da barra.
Passo 3
Podemos analisar o nó F, pois só sobraram duas forças desconhecidas:
Agora vamos montar as equações.
Para :
Nós já descobrimos o valor de :
Já que a sentinha sai da seção da barra.
Agora vamos olhar para o eixo :
Nós já sabemos quanto vale e :
A sentinha na real está entrando na seção da barra.
Passo 4
Vamos analisar o nó D:
Eixo :
Sabemos o valor de :
Eixo :
Tirando o cosseno em evidência
Vamos somar essa equação com a que encontramos para o eixo :
Substituindo em qualquer uma das duas equações acima:
Passo 5
E finalmente, vamos analisar o nó B, e com isso descobrimos todas as forças:
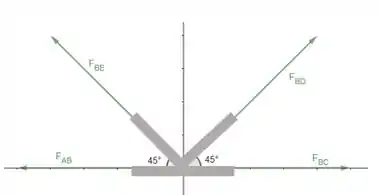
Fazendo o somatório das forças para o eixo :
A única força que não temos dessa equação é , substituindo as outras vamos ter: