Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 48

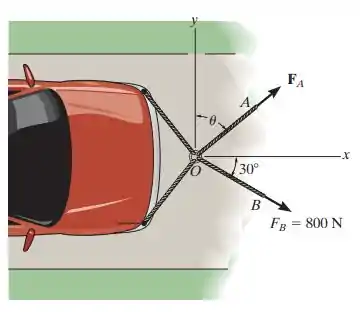
2.48. Determine a intensidade e a direção medida no sentido anti-horário a partir do eixo x positivo da força resultante que atua sobre o anel em O se F A = 750   N e θ = 45 ° .

Passo 1

O exercício pede para a gente determinar a intensidade e a direção de F R . Para isso vamos decompor as forças em termos dos eixos x e y para facilitar os cálculos, aí poderemos determinar a componente da força resultante no eixo x e depois a componente no eixo y e soma-las vetorialmente.

Passo 2

Vamos começar por F R x

F R x = F A x + F B x

F R x = 750 ⋅ sin ⁡ 45 ° + 800 ⋅ cos ⁡ 30 °

F R x = 1223,15

Agora vamos fazer a mesma coisa para F R y

F R y = F A y + F B y

F R y = 750 ⋅ cos ⁡ 45 ° - 800 ⋅ sin ⁡ 30 °

F R y = 130,33

Passo 3

Agora podemos representar a situação vetorialmente da seguinte maneira

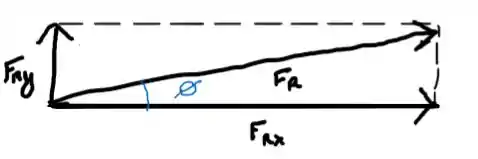
Vamos somar vetorialmente para obter F R

F R 2 = F R x 2 + F R y 2

F R 2 = 1223,15 2 + 130,33 2

F R = 1513,08 = 1230   N

Passo 4

Repare que da representação vetorial podemos extrair o seguinte triângulo

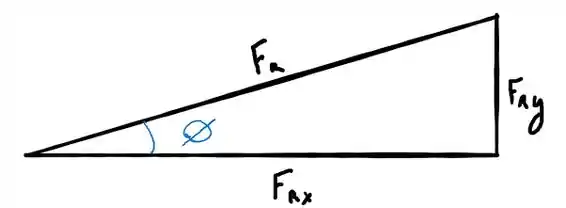
E para determinar Φ , basta lembrar que

tan ⁡ Φ = c a t e t o   o p o s t o c a t e t o   a d j a c e n t e = F R y F R x = 130,33 1223,15

Então

Φ = t a n - 1 130,33 1223,15 = 6,08 °

Resposta

F R = 1230   N θ = 6,08 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No projeto de um mecanismo de controle é determinado que a barra A B transmite uma força P de 260N à manivela B C . Determine os componentes escalares x e y de P .
O módulo da força F é 6 00N . Expresse F como um vetor, em termos dos vetores unitáriosi e j . Identifique os componentes escalares e vetoriais de F .
Os dois elementos estruturais, um sob tração e o outro sob compressão, exercem as forças indicadas no nó O . Determine o módulo da resultante R das duas forças e o ângulo θ que R faz com o eixo x posi
Um cabo esticado entre os suportes fixos A e B está sob uma tração T de 900N . Usando os vetores unitários i e j expresse a tração como um vetor; primeiramente como uma força T A atuando em A e, em se
Determine o módulo F s da força trativa atuando na mola, para que a resultante de F s e de F seja uma força vertical. Determine o módulo R dessa força resultante vertical.