Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.3 - Ex. 7
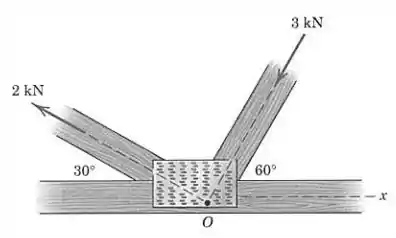
Os dois elementos estruturais, um sob tração e o outro sob compressão, exercem as forças indicadas no nó . Determine o módulo da resultante das duas forças e o ângulo que faz com o eixo positivo.
Passo 1
Primeiro, somamos todas as componentes de força em , a fim de determinar o módulo da resultante nessa direção:
E agora, em :
Passo 2
Show! Agora vamos lembrar que o módulo de uma força se calcula assim:
E o ângulo é calculado assim:
Como as duas componentes e são negativas, o ângulo deve estar no quadrante, portanto:
Resposta
Exercícios de Livros Relacionados
As três forças concorrentes que atuam sobre o poste produzem uma força resultante F R = 0 . Se F 2 = 1 2 F 1 e F 1 estiver a 90 ° de F 2 , como mostra a figura, determine a intensidade necessária de F
Se a intensidade da força resultante que atua sobre o suporte deve ser 450N direcionada ao longo do eixo u positivo, determine a intensidade de F 1 e sua direção ϕ .
Especifique a intensidade de F 3 e seus ângulos de direção coordenados α 3 , β 3 , γ 3 de modo que a força resultante seja F R = { 9 j } kN.
2.6. Se a força F precisa ter uma componente ao longo do eixo u com F u = 6k N , determine a intensidade de F e de sua componente F v ao longo do eixo v.
2.3. A força F = 900N atua sobre a estrutura. Decomponha essa força nas componentes que atuam ao longo dos membros AB e AC, e determine a intensidade de cada componente.