Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 105

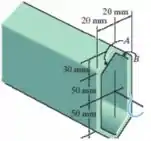
O tubo é feito de plástico, tem 5mm de espessura e as dimensões médias são mostradas na figura. Determine a tensão de cisalhamento média nos pontos A e B se o tubo for submetido a um torque T = 500   N ⋅ m . Mostre a tensão de cisalhamento em elementos de volume localizados nesses pontos. Despreze as concentrações de tensão nos cantos.

Passo 1

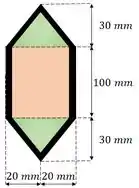
Para reseolver este problema basta aplicar a Equação 5.18. Mas antes, precisamos calcular a área contida na figura. Veja a figura abaixo, precisamos calcular a soma da área verde com a área laranja.

Vale notar, que pelas dimensões da seção transversal serem muito maiores que a espessura da parede fina, então podemos desconsiderar a espessura no cálculo da área.

A m = 1 2 ⋅ 30 ⋅ 40 + 100 ⋅ 40 + 1 2 30 ⋅ 40

A m = 5200   m m 2

Passo 2

Agora basta aplicar a Equação 5.18

τ A = T 2 ⋅ t ⋅ A m

τ A = 500 2 ⋅ 5 ⋅ 5200 ⋅ N ⋅ m m m ⋅ m m 2

τ A = 500 2 ⋅ 5 ⋅ 5200 ⋅ N ⋅ ( 10 3 ⋅ m m ) m m ⋅ m m 2

τ A = 500 ⋅ 10 3 2 ⋅ 5 ⋅ 5200 ⋅ N ⋅ m m m m ⋅ m m 2

τ A = 9.62   M P a

Passo 3

Por serem simétricos e por terem a mesma espessura, os pontos A e B sofrem a mesma tensão

τ b = τ A = 9.62   M P a

Resposta

τ A = 9.62   M P a

τ B = 9.62   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma escora de alumínio 2014 - T 6 está presa entre duas paredes A e B . Se tiver seção transversal quadrada de 50m m por 50m m e for submetida ao carregamento de torção mostrado, determine as reações
Determine o torque T que pode ser aplicado ao tubo retangular se a tensão de cisalhamento média não pode ultrapassar 84M P a . Despreze as concentrações de tensão nos cantos. As dimensões médias do tu
Pretende-se fabricar uma barra circular para resistir a torque; todavia, durante o processo de fabricação, a barra ficou elíptica, sendo que uma dimensão ficou menor que a outra por um fator k, como m
O tubo de aço inoxidável 304 tem espessura de 10m m . Se o torque aplicado for T = 50N ⋅ m , determine a tensão de cisalhamento média no tubo. Despreze as concentrações de tensão nos cantos. As dimens
O eixo quadrado é usado na extremidade de um cabo de acionamento para registrar a rotação do cabo em um medidor. Se tiver as dimensões mostradas na figura e for submetido a um torque de 8N ⋅ m , deter