Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 3.Problemas - Ex. 40
Ao ser submetido a um ensaio de tração, um corpo de prova de liga de cobre com comprimento de referência de sofre uma deformação de quando a tensão é de . Se quando , determine a distância entre os pontos de referência quando a carga é aliviada.
Passo 1
Oláaaa, querido! Tá bem?
Então, a gente tem um corpo de prova sendo tracionado.
A gente quer encontrar o valor da distância entre os pontos de referência quando essa carga for aliviada, ou seja, queremos encontrar o valor da distância entre os pontos de referência quando a carga deixa de ser aplicada com toda sua intensidade.
Mas repara que a tensão nele chega , que é maior que a tensão de escoamento . Ou seja, a deformação que ele sofre não vai ser só elástica, e haverá uma deformação permanente depois que não houver mais carregamento.
É essa deformação permanente que a gente quer para saber a distância final entre os ponto de referência. Cê pode imaginar que essa distância entre pontos de referência é como se fosse a altura do corpo de prova. Bora lá!
Passo 2
Primeiro a gente precisa do módulo de elasticidade do material. Ele disse que na tensão de escoamento a deformação é . Esse ponto é o limite do regime elástico, então a gente pode usar a lei de Hooke nele
Isolando o módulo de elasticidade e substituindo nossos dados:
Passo 3
E para que a gente queria esse carinha? Olha esse gráfico aqui para ilustrar:
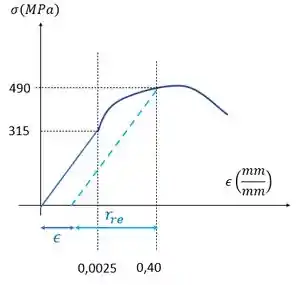
Então, quando a gente passa do ponto da tensão de escoamento, começamos a ter uma deformação permanente. E como a gente sabe o valor dela? Acontece é que se a tensão for tirada, o corpo vai se recuperar através da reta azul tracejada. Como assim?
Ele vai sair do ponto onde e voltar ao ponto , mas no eixo horizontal, ele não vai estar em , mas em marcado de azul, a deformação permanente. E aí a gente acha esse valor sabendo que a reta tracejada e a reta continua têm a mesma inclinação.
Isso diz que as duas tem o mesmo coeficiente linear, o módulo ! Por isso, conseguimos calcular o coeficiente de recuperação elástica como sendo
Dessa forma, podemos calcular a deformação permanente:
Passo 4
Por fim, podemos encontrar o alongamento permanente para a então encontrarmos a distância entre os pontos de referência. Temos que
Isolando o alongamento e substituindo nossos valores, sabendo que a distância inicial entre pontos de referência é .
A distância entre os pontos de referencia vai ser a distância inicial mais o alongamento permanente: