Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 10.Problemas - Ex. 67
Uma coluna com 6,4m de comprimento efetivo é obtida conectando quatro cantoneiras de aço L89 x 89 x 9,5mm com barras de travamento conforme mostrado. Utilizando método das tensões admissíveis, determine a carga centrada admissível para a coluna. Utilize
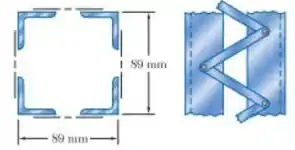
Passo 1
Galerinha, vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo: Mas antes vamos ao nosso velho e querido esboço :D
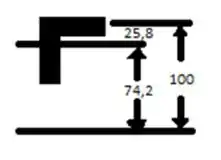
Então vamos aos dados do enunciado, partiu?
Passo 2
Temos que o diâmetro é dado por:
E agora temos que determinar a inércia :D
A área é obtida por:
E a razão comprimento/ raio é dada por:
Passo 3
Agora partiu determinar as tensões :D
E a força P é dada por:
Resposta
.
Exercícios de Livros Relacionados
Uma coluna de comprimento flambagem de 685,8m m deve suportar uma força centrada central de 1821k N . Usando o método de tensão admissível selecione o perfil de mesa larga de 360m m de altura nominal
Uma coluna de comprimento flambagem de 17f t deve suportar uma força centrada central de 235k i p s . Usando o método de tensão admissível selecione o perfil de mesa larga de 10i n de altura nominal q
Um tubo estrutural quadrado com a seção transversal mostrada é usado como uma coluna de 6096m m de comprimento de flambagem para suportar uma força centrada de 289k N . Sabendo que os tubos disponívei
Duas cantoneiras de 89m m×64m m são soldadas como mostra a figura, para formarem uma coluna de flambagem de 2,4m para suportar uma força centrada de 325k N . Sabendo que as cantoneiras disponíveis t
Usando o método da tensão admissível, determine a força centrada admissível para uma coluna com comprimento de flambagem de 6m feita com os seguintes perfis de aço laminado: (a) W200 x 35,9 e (b) W200