Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 72
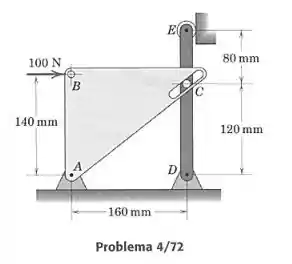
Calcule o módulo da força atuando no pino em . O pino está preso em e desliza no rasgo liso existente na placa triangular.
Passo 1
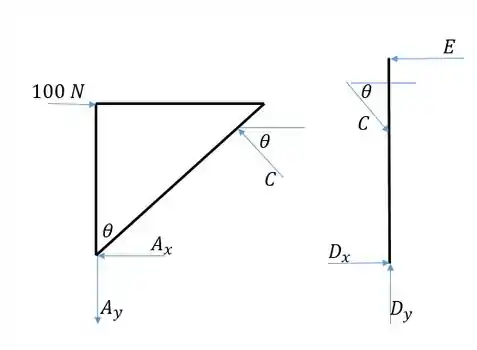
Vamos encontrar a força fazendo o diagrama de corpo livre para cada corpo e resolvendo as equações de equilíbrio. A gente deve prestar atenção às forças de ação e reação entre os corpos. Vamos desconsiderar os pinos, fazendo como se o triângulo fizesse força diretamente na barra .
Passo 2
Temos para a barra 4 forças desconhecidas, então não conseguimos resolver as equações só com essa barra. Precisamos achar a força através do triângulo. Achamos ela diretamente calculando o momento em torno de , pois evitamos as forças desconhecidas nesse ponto e trabalhamos apenas com como incógnita. A distância é:
Então:
Passo 3
Agora aplicamos na barra o momento em relação a , para encontrar a força diretamente:
Substituindo e o valor do cosseno:
Agora fazemos os equilíbrio vertical e horizontal para encontrar as forças em :
O sinal negativo indica que a força é para a esquerda e não para a direita. Agora o vertical:
Substituindo o valor do seno e o valor de :
Passo 4
Basta então pra gente calcular o módulo da força: