Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 74
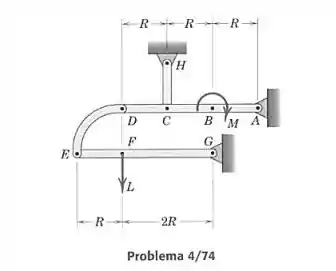
Para qual valor do momento a força no elo será nula, dados os valores da carga e da dimensão .
Passo 1
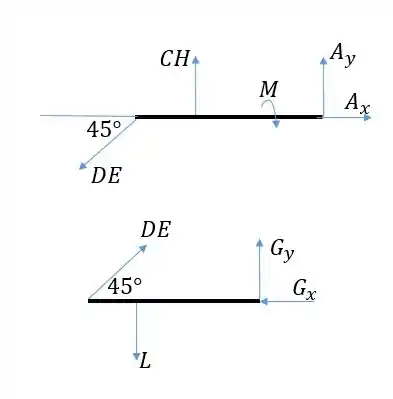
Vamos analisar as forças e momentos do problema isolando os elementos e . Não precisamos representar porque o tratamos omo um elemento de duas forças, como se fosse uma barra retilínea inclinada de 45° com a horizontal.
Passo 2
Sendo , temos 4 incógnitas na barra de cima, então não conseguimos resolver só com as equações de equilíbrio dessa barra. Devemos obter o valor de através das equações da barra de baixo. Se fizermos o momento em relação a na barra de baixo as forças desconhecidas de não aparecem, então achamos diretamente:
Agora que temos , achamos através da soma das forças verticais na barra de cima:
Substituindo o valor de :
Agora que já temos todas as forças verticais da barra, podemos fazer com que o momento em torno de , onde é aplicado , seja igual a zero:
Colocamos pois o momento é no sentido horário. Agora substituindo as forças: