Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 71
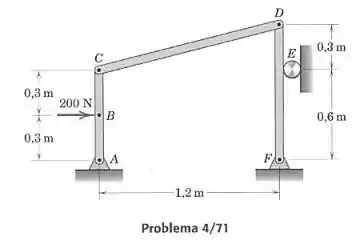
Determine a força suportada pelo rolete em E.
Passo 1
Como a estrurura não é rígida, vamos encontrar a força fazendo o diagrama de corpo livre para cada corpo e resolvendo as equações de equilíbrio. A gente deve prestar atenção às forças de ação e reação entre os corpos. Vamos desconsiderar os pinos, fazendo como se fosse as barras fazendo força diretamente nas outras.
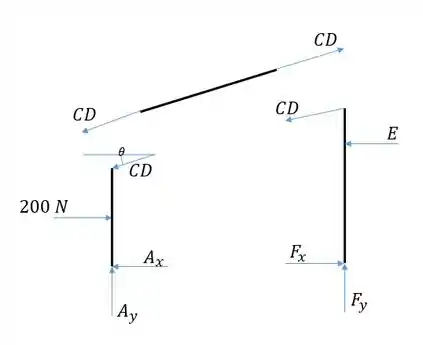
Passo 2
Temos como incógnitas na barra da direita , , e . Olhando para a da esquerda, vemos que conseguimos obter através de uma equação de momento em torno de , pois e não aparecerão na conta.
Do triangulo BCE, temos:
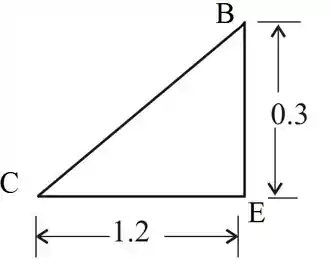
Então achamos o valor de :
Passo 3
Agora aplicamos na barra da direita o momento em relação a , para evitar as forças em :
Resposta
Exercícios de Livros Relacionados
Antes que o tronco de uma grande árvore venha a cair, são amarrados cabos AB e BC, como mostra a figura. Sabendo que as forças de tração nos cabos AB e BC são de 555N e 660N , respectivamente, determi
134. Resolva o Problema 4.133 , considerando que o cabo D F é substituído por um cabo que conecte B e F .
135. A placa A B C D de 50k g é sustentada por dobradiças ao longo de A B e pelo arame C E . Sabendo que a placa é uniforme, determine a tração no arame.
133. A haste dobrada A B D E é apoiada por rótulas em A e E e pelo cabo D F . Se uma carga de 240N é aplicada em C , tal como mostra a figura, determine a tração no cabo.
131. A montagem mostrada na figura consiste em uma barra A F de 80m m que é soldada a uma cruz representada por quatro braços de 200m m . A montagem é mantida por uma rótula em F e por três conexões c