Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 83

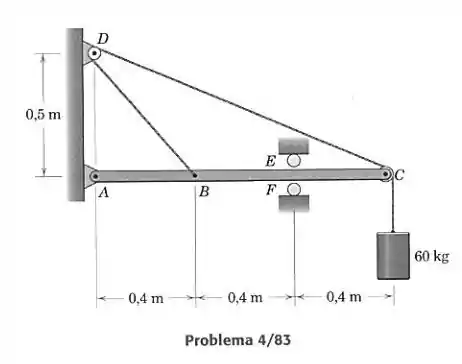
Determine o módulo da reação do pino em A e o módulo e a direção da força de reação nos roletes. As polias em C e D são pequenas.

Passo 1

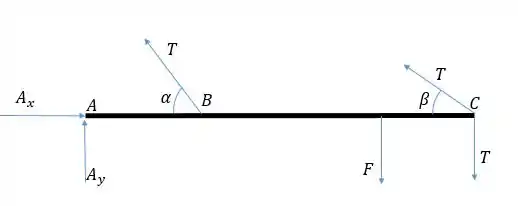
Isolando a barra A C em um diagrama de corpo livre, vemos as forças às quais ela está sujeita. Vamos considerar que a polia em C faz parte da barra. Todas as forças feitas pelo fio têm o mesmo módulo T (mesmo fio, mesma tração!):

Passo 2

A tração T suporta o peso de 60 kg, então:

T = 60 g

Vamos agora encontrar o seno e o cosseno dos ângulos α e β que serão importantes para nossas equações. Primeiro α :

B D - = 0,5 2 + 0,4 2 = 0,41 = 0,64

sin ⁡ α = 0,5 0,64 = 0,7809   ;       cos ⁡ α = 0,4 0,64 = 0,6247

Agora para β :

C D - = 0,5 2 + 1,2 2 = 1,69 = 1,3

sen ⁡ β = 0,5 1,3 = 0,3846   ;         cos ⁡ β = 1,2 1,3 = 0,9231

Passo 3

Para encontrar a força F , fazemos o momento em torno de A :

∑ M A = 0 ⇒ T sen ⁡ α 0,4 - F 0,8 - T 1,2 + T sen ⁡ β 1,2 = 0

Substituindo T e os senos:

0,7809 × 60 g ( 0,4 ) - 0,8 F - 60 g 1,2 + 0,3846 × 60 g 1,2 = 0

⇒ 18,74 g - 0,8 F - 72 g + 27,69 g = 0

Passando 0,8 F pro outro lado:

18,74 g - 72 g + 27,69 g = 0,8 F ⇒ 0,8 F = - 25,57 g

⇒ F = - 25,57 g 0,8 = - 31,96 g

O sinal negativo indica que a força é para cima e não para baixo como desenhamos. Se g = 9,81   m / s 2 :

F = 31,96 × 9,81 = 313,6   N   ( p a r a   c i m a )

Passo 4

Agora que as únicas incógnitas são as forças em A , as achamos fazendo os equilíbrios vertical e horizontal na barra:

∑ F x = 0 ⇒ A x - T cos ⁡ α - T cos ⁡ β = 0

⇒ A x = 60 g 0,6247 + 0,9231 = 92,87 g = 911   N

∑ F y = 0 ⇒ A y + T sen ⁡ α + F + T sen ⁡ β - T = 0

⇒ A y = T 1 - sen ⁡ α - sen ⁡ β - F = 60 g 1 - 0,7809 - 0,3846 - 31,96 g

⇒ A y = - 41,89 g = - 411   N

Agora encontramos o módulo da força em A :

A = A x 2 + A y 2 = 911 2 + 411 2 = 999,4   N

Resposta

F = 313,6   N   ( p a r a   c i m a )

A = 999,4   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O elemento curvo encontra-se no plano x-y e possui um raio de 3 m. Se uma força F = 80 N atua emsua extremidade, como mostra a figura, determine o momento dessa força em relação ao ponto B.Fonte: Está
O encanamento está sujeito à força de F = {600i + 800j - 500k} N. Determine o momento dessa força em relação ao ponto B.Fonte: Estática Mecânica para Engenharia – 14ª ed
Uma força F com intensidade F = 100 N age ao longo da diagonal do paralelepípedo. Determine omomento de F em relação ao ponto A, usando M A = r B × F e M A = r C × F .Fonte: Estática Mecânica para Eng
42. Determine o momento resultante produzido pelas forças F B → e F C → em relação ao ponto O. Expresse o resultado como um vetor cartesiano.
Uma força F = {6i - 2j + 1k} kN produz um momento M O = {4i + 5j - 14k} kN m em relação à origem das coordenadas, o ponto O. Se a força age em um ponto tendo uma coordenada x de x = 1 m, determine as