Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 100
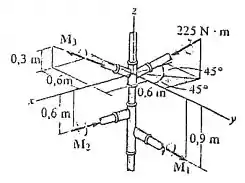
Se , e , determine a intensidade e os ângulos de direção coordenados do momento de binário resultante.
Passo 1
O problema pede para acharmos o binário resultante. Note que além dos binários , e dados no problema, tem um quarto binário na figura, com
com . Desta forma, temos que
Além disso, temos
Para o binário , note que ele está na direção do vetor que é a mesma direção do vetor , cuja norma é . Assim,
Passo 2
O binário resultante será dado por:
Assim, teremos:
Passo 3
Substituindo , , e , vamos encontrar:
Assim, a intensidade do binário resultante será
Resposta
Exercícios de Livros Relacionados
Se a resultante das três forças é F r = - 4,5 kk N , determine a intensidade da força em cada corrente.
As forças e binários mostrados na figura são aplicados em dois parafusos à medida que uma chapa metálica é parafusada em um bloco de madeira. Reduza as forças e os binários a um torsor equivalente e d
Dois parafusos A e B são apertados aplicando-se as forças e os binários mostrados na figura. Substitua os dois torsores por um torsor único equivalente e determine a a resultante R , b o passo do tors
Uma peça de chapa metálica é dobrada no formato mostrado e sofre a ação de três forças. Se as forças tem a mesma intensidade P , substitua as três forças por um torsor equivalente e determine a a inte
Dois parafusos A e B são apertados aplicando-se as forças e os binários mostrados na figura. Substitua os dois torsores por um torsor único equivalente e determine a a resultante R , b o passo do tors