Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 33
3.33. O fio forma um contorno fechado e passa pelas pequenas polias em A, B, C e D. Se sua extremidade está submetida a uma força de , determine a força no fio e a intensidade da força resultante exercida pelo fio em cada polia.
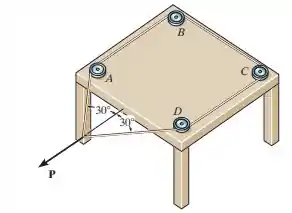
Passo 1
Vamos determinar os eixos dessa forma
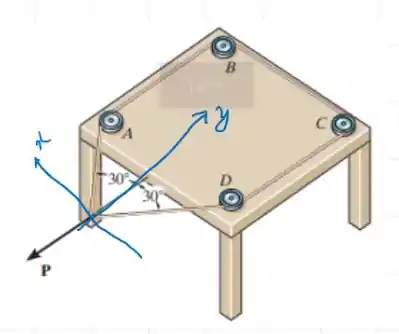
E aí podemos usar as equações de equilíbrio para os eixos x e y.
Passo 2
Vamos usar as condições de equilíbrio para o eixo y
Passo 3
Agora vamos calcular para A e D
Passo 4
Agora vamos calcular para B e C
Resposta
Exercícios de Livros Relacionados
O cursor A é ligado a uma carga de 220 N e pode deslizar sem atrito sobre a barra horizontal. Determine a distância x para que o cursor esteja em equilíbrio quando P = 210N .
Solucione as partes b e d do Problema 2.67 considerando que o lado livre da corda está preso ao caixote.
Dois cabos ligados em C são carregados como mostra a figura. Sabendo que a tração máxima admissível é de 1200 N no cabo AC e 600 N no cabo BC, determine ( a ) a maior intensidade da força P que pode s
Sabendo que as porções AC e BC do cabo ACB devem ser iguais, determine o menor comprimento do cabo que pode ser usado para suportar a carga mostrada se a tração no cabo não puder exceder 870 N.
Um caixote de 2670 N é sustentado por vários sistemas de corda e roldana como mostra a figura. Determine para cada caso a tração na corda. (Ver a dica do Problema 2.65.)